Cyber Apocalypse CTF 2021 | Part 1
This week possibly the biggest cybersecurity Capture The Flag (CTF) ever was held as a joint event between HackTheBox and CryptoHack. With 9900 players participating in 4740 teams; plentiful prizes including cash and swag; and donations to charity for each challenge solved, this was a fantastic event to be part of.

The theme was that Earth is being hacked by malicious extraterrestrials. By solving a series of challenges, humans could fight back and save the planet. CryptoHack provided the cryptography challenges, which were themed around rescuing classic video games from the aliens:
The aliens have encrypted all our games to try and force us to be productive. Fortunately, the aliens haven’t played CryptoHack so don’t know how to make a strong cipher. Can you recover our games, consoles, and flags?
Thanks especially to r0adrunn3r and makelaris who were welcoming and worked closely with us during the creation of the challenges and planning of the competiton.
We spent approximately a month writing the challenges and playtesting the puzzles before sending them to HTB to be hosted on their beautiful platform. On the whole, the challenges held up well against the fury of almost 10k CTF players, although there were a couple unintended solutions reported along the way which we discuss here along with the intended solutions.
You can find all of our files relating to these challenges on our Github repo, if you’re interested.
We’ve been talking in the discord about potentially developing a new section on the main site as an archive for CTF challenges. If this is something interesting, come chat with us about it. Potentially this set of 17 challenges could be a good excuse to kick-start the archive.
Contents
| Challenge Name | Category | Difficulty | Solves |
|---|---|---|---|
| Nintendo Base64 | Encoding | Easy | 1928 |
| PhaseStream | XOR Encryption | Easy | 1217 |
| PhaseStream 2 | XOR Encryption | Easy | 919 |
| PhaseStream 3 | AES CTR | Easy | 531 |
| SoulCrabber | 🦀 / RNG | Easy | 432 |
| PhaseStream 4 | AES CTR | Medium | 334 |
| SoulCrabber II | 🦀 / RNG | Medium | 229 |
| RSA Jam | Carmichael lambda | Medium | 146 |
| Super Metroid | Elliptic group order | Medium | 77 |
| Forge of Empires | Elgamal message forgery | Medium | 95 |
| Tetris | Classical ciphers | Medium | 75 |
| Little Nightmares | Fermat’s little theorem | Medium | 86 |
| Wii Phit | Erdős-Straus conjecture | Hard | 38 |
| RuneScape | Imai-Matsumoto implementation | Insane | 20 |
| Tetris 3D | Classical ciphers | Insane | 18 |
| Hyper Metroid | Hyperelliptic group order | Insane | 18 |
| SpongeBob SquarePants | Sponge hash collision | Insane | 61 |
Easy
For the easy section, we only give a brief overview of the challenge and solution. We expect that there will be many community generated writeups for these challenges due to the higher number of solves. For new players who found these challenges mystifying, playing through CryptoHack is a perfect space to get more familiar with the techniques required to solve these.
Nintendo Base64
Author: Hyperreality
Aliens are trying to cause great misery for the human race by using our own cryptographic technology to encrypt all our games.
Fortunately, the aliens haven’t played CryptoHack so they’re making several noob mistakes. Therefore they’ve given us a chance to recover our games and find their flags. They’ve tried to scramble data on an N64 but don’t seem to understand that encoding and ASCII art are not valid types of encryption!
In this challenge, we get a nice ASCII art picture of “nintendo64x8”. Going by the name of the challenge and the text we see, we can observe that all characters used belong to the base64 alphabet. Removing all whitespace and base64-decoding 8 times, we can quickly obtain the flag.
PhaseStream
Author: Hyperreality
The aliens are trying to build a secure cipher to encrypt all our games called “PhaseStream”. They’ve heard that stream ciphers are pretty good.
The aliens have learned of the XOR operation which is used to encrypt a plaintext with a key. They believe that XOR using a repeated 5-byte key is enough to build a strong stream cipher. Such silly aliens!
Here’s a flag they encrypted this way earlier. Can you decrypt it (hint: what’s the flag format?)
2e313f2702184c5a0b1e321205550e03261b094d5c171f56011904
First notice that the given ciphertext is hex-encoded, as that is a clean way to nicely represent unprintable bytes. Of course we’ll have to decode this first before we do anything else.
From there, we know the repeating-xor key is 5 bytes long, and from the flag format, we know the first 5 bytes will be CHTB{. Since xor is its own inverse, commutative and associative, we can find the 5 key bytes simply by taking xor("CHTB{", decode_hex("2e313f2702")). This turns out to be the key mykey.
Applying this key to the entire given ciphertext gives us the flag.
Flag
CHTB{u51ng_kn0wn_pl41nt3xt}
PhaseStream 2
Author: Hyperreality
The aliens have learned of a new concept called “security by obscurity”. Fortunately for us they think it is a great idea and not a description of a common mistake.
We’ve intercepted some alien comms and think they are XORing flags with a single-byte key and hiding the result inside 9999 lines of random data, Can you find the flag?
There are 10000 lines, only one of which contains the flag. We can quickly script the loop through the lines, and test each line if it starts with CHTB{ after xor with every single-byte key.
Note that we can apply the same technique as in PhaseStream1 to identify the correct key byte by xoring the first ciphertext byte with C, and that we thus don’t need to try all possible keys.
Implementation
def xor(a, b):
res = []
i = 0
while i < len(a) or i < len(b):
res.append(a[i % len(a)] ^ b[i % len(b)])
i += 1
return bytes(res)
for l in open("output.txt").read().strip().splitlines():
t = bytes.fromhex(l)
s = xor(t, xor(t[:1], b'C'))
if s.startswith(b"CHTB"):
print(s.decode())
Flag
CHTB{n33dl3_1n_4_h4yst4ck}
PhaseStream 3
Author: Hyperreality
The aliens have learned the stupidity of their misunderstanding of Kerckhoffs’s principle.
Now they’re going to use a well-known stream cipher (AES in CTR mode) with a strong key. And they’ll happily give us poor humans the source because they’re so confident it’s secure!
Challenge
from Crypto.Cipher import AES
from Crypto.Util import Counter
import os
KEY = os.urandom(16)
def encrypt(plaintext):
cipher = AES.new(KEY, AES.MODE_CTR, counter=Counter.new(128))
ciphertext = cipher.encrypt(plaintext)
return ciphertext.hex()
test = b"No right of private conversation was enumerated in the Constitution. I don't suppose it occurred to anyone at the time that it could be prevented."
print(encrypt(test))
with open('flag.txt', 'rb') as f:
flag = f.read().strip()
print(encrypt(flag))
Solution
AES-CTR is a mode of operation for AES that turns it into a stream cipher. That is, it generates a keystream that will then be xored against the plaintext to encrypt it.
The problem in this challenge is that the counter is improperly initialized, and because of that, the keystream will be identical across encryptions.
That means we can recover the keystream from known plaintext, just like we did for PhaseStream 1 - but with a longer known plaintext and a longer keystream.
Implementation
from pwn import xor
a = bytes.fromhex("08501b3dbd0fb2f7c87aeb3a224a9d568fa8ad83ff442548b5f4334f0fe1dd6b8f5d5e410be5af2d7ea642b12d8f459f2ab666d4f79a9115dc9cf22ed60e899769fd206c40819bbefe2b5a2ec592a387c6927d866b6343466d5effde0666dd3bb7f657ed651bfcf45fd5b264a36406c6b6dbb1a81272029c5e06da438a0281c19c1e10a0dc47d6ae994557e82663e9f59578")
b = bytes.fromhex("05776f0daf1ae9f6dd26e945390bad7fda889c97ff6036")
test = b"No right of private conversation was enumerated in the Constitution. I don't suppose it occurred to anyone at the time that it could be prevented."
key = xor(a, test)
print(xor(key, b))
Flag
CHTB{r3u53d_k3Y_4TT4cK}
SoulCrabber
Author: Hyperreality
Aliens heard of this cool newer language called Rust, and hoped the safety it offers could be used to improve their stream cipher.
Challenge
use rand::{Rng,SeedableRng};
use rand::rngs::StdRng;
use std::fs;
use std::io::Write;
fn get_rng() -> StdRng {
let seed = 13371337;
return StdRng::seed_from_u64(seed);
}
fn rand_xor(input : String) -> String {
let mut rng = get_rng();
return input
.chars()
.into_iter()
.map(|c| format!("{:02x}", (c as u8 ^ rng.gen::<u8>())))
.collect::<Vec<String>>()
.join("");
}
fn main() -> std::io::Result<()> {
let flag = fs::read_to_string("flag.txt")?;
let xored = rand_xor(flag);
println!("{}", xored);
let mut file = fs::File::create("out.txt")?;
file.write(xored.as_bytes())?;
Ok(())
}
Solution
We are given the encrypted flag as hex bytes in a file called out.txt. To solve the challenge all we need to do is encrypt the string again using the known seeded pseudo-random keystream since flag ^ key ^ key = flag.
🦀 Welcome to Rust! 🦀
use rand::rngs::StdRng;
use rand::{Rng, SeedableRng};
use std::char;
use std::fs;
fn get_rng(seed: u64) -> StdRng {
return StdRng::seed_from_u64(seed);
}
fn rand_xor(seed: u64, input: &Vec<u8>) -> String {
let mut rng = get_rng(seed);
return input
.into_iter()
.map(|c| char::from_u32((c ^ rng.gen::<u8>()) as u32).unwrap())
.collect::<String>();
}
fn main() {
let enc_flag = fs::read_to_string("out.txt").expect("Something went wrong reading the file");
let enc_flag = hex::decode(enc_flag).expect("Decoding failed");
let flag = rand_xor(13371337, &enc_flag);
println!("{}", flag);
}
// CHTB{mem0ry_s4f3_crypt0_f41l}
Flag
CHTB{mem0ry_s4f3_crypt0_f41l}
Medium
PhaseStream 4
Author: Hyperreality
The aliens saw us break PhaseStream 3 and have proposed a quick fix to protect their new cipher.
Challenge
from Crypto.Cipher import AES
from Crypto.Util import Counter
import os
KEY = os.urandom(16)
def encrypt(plaintext):
cipher = AES.new(KEY, AES.MODE_CTR, counter=Counter.new(128))
ciphertext = cipher.encrypt(plaintext)
return ciphertext.hex()
with open('test_quote.txt', 'rb') as f:
test_quote = f.read().strip()
print(encrypt(test_quote))
with open('flag.txt', 'rb') as f:
flag = f.read().strip()
print(encrypt(flag))
Solution
The key to solving this challenge is the following observation: if $C_a = a \oplus k$ and $C_b = b \oplus k$, then $C = C_a \oplus C_b = a \oplus b$ and the key has entirely disappeared. This means that we can try to find a piece of known (or guessed) plaintext in either $a$ or $b$, and test if we get reasonable plaintext in when we xor it against $C$. If we do, we might be able to extend the known/guessed plaintext for the other plaintext and repeat this process.
This is known as crib dragging and there even exist some useful tools online that might be able to help us solve this, such as this one.
After some trial and error, we can get a partial quote, google it and find the complete quote, which we then use to find the flag. We just need to be careful as the punctuation of the quote might not be the same everywhere, and might not exactly match the one used in the challenge. To fix problems like that, simply find the first place where the flag starts going wrong and experiment from there.
Flag
CHTB{stream_ciphers_with_reused_keystreams_are_vulnerable_to_known_plaintext_attacks}
SoulCrabber II
Author: Hyperreality
Aliens realised that hard-coded values are bad, so added a little bit of entropy.
Challenge
use rand::{Rng,SeedableRng};
use rand::rngs::StdRng;
use std::fs;
use std::io::Write;
use std::time::SystemTime;
fn get_rng() -> StdRng {
let seed = SystemTime::now()
.duration_since(SystemTime::UNIX_EPOCH)
.expect("Time is broken")
.as_secs();
return StdRng::seed_from_u64(seed);
}
fn rand_xor(input : String) -> String {
let mut rng = get_rng();
return input
.chars()
.into_iter()
.map(|c| format!("{:02x}", (c as u8 ^ rng.gen::<u8>())))
.collect::<Vec<String>>()
.join("");
}
fn main() -> std::io::Result<()> {
let flag = fs::read_to_string("flag.txt")?;
let xored = rand_xor(flag);
println!("{}", xored);
let mut file = fs::File::create("out.txt")?;
file.write(xored.as_bytes())?;
Ok(())
}
Solution
This is a very similar challenge to SoulCrabber I, but now the RNG is seeded with the time that the flag was encrypted. To solve this challenge, we need to count backwards in time, trying all seeds until we find the flag.
We implement this with the function brute_seed() with most of the code being reused from the last challenge.
use rand::rngs::StdRng;
use rand::{Rng, SeedableRng};
use std::char;
use std::fs;
use std::time::SystemTime;
fn get_rng(seed: u64) -> StdRng {
return StdRng::seed_from_u64(seed);
}
fn rand_xor(seed: u64, input: &Vec<u8>) -> String {
let mut rng = get_rng(seed);
return input
.into_iter()
.map(|c| char::from_u32((c ^ rng.gen::<u8>()) as u32).unwrap())
.collect::<String>();
}
fn brute_seed(input: Vec<u8>) -> String {
let mut seed = SystemTime::now()
.duration_since(SystemTime::UNIX_EPOCH)
.expect("Time is broken")
.as_secs();
loop {
let flag = rand_xor(seed, &input);
if flag.contains("CHTB{") {
return flag;
} else {
seed = seed - 1;
}
}
}
fn main() {
let enc_flag = fs::read_to_string("out.txt").expect("Something went wrong reading the file");
let enc_flag = hex::decode(enc_flag).expect("Decoding failed");
let flag = brute_seed(enc_flag);
println!("{}", flag);
}
// CHTB{cl4551c_ch4ll3ng3_r3wr1tt3n_1n_ru5t}
Flag
CHTB{cl4551c_ch4ll3ng3_r3wr1tt3n_1n_ru5t}
RSA Jam
Author: Robin
Even aliens have TLA agencies trying to apply rubber hose cryptanalysis.
Challenge
from Crypto.Util.number import getPrime, inverse
import random
def main():
print("They want my private key, but it has sentimental value to me. Please help me and send them something different.")
p = getPrime(512)
q = getPrime(512)
N = p*q
phi = (p - 1) * (q - 1)
e = 0x10001
d = inverse(e, phi)
print({'e': e, 'd': d, 'N': N})
d2 = int(input("> "))
assert d2 != d
assert 0 <= d2 < phi
with open("flag.txt") as f:
flag = f.read()
random.seed(str(d2) + flag)
for _ in range(50):
m = random.randrange(N)
c = pow(m, e, N)
assert m == pow(c, d2, N)
print(flag)
if __name__ == "__main__":
import os
os.chdir(os.path.abspath(os.path.dirname(__file__)))
main()
Solution
We’re presented with a scenario where we need to produce a decryption exponent $d’$ for an RSA challenge that’s:
- not the classical $d = e^{-1} \pmod{\varphi(n)}$
- not a trivial variant $d’ = d + k\varphi(n)$
and this will lead us into a short discussion about the exact workings of RSA decryption.
Usually, when dealing with RSA, we look at the Euler totient of the modulus $\varphi(N)$ (in the most common form for RSA, with two primes, $\varphi(N) = \varphi(pq) = (p - 1)(q - 1)$). If we consider the group $\mathcal{G} = (\mathbb{Z}/N\mathbb{Z})^{\star}$ (the multiplicative group of invertible elements mod $N$) to be the fundamental object we are working with in RSA, we know that the order of $\mathcal{G}$ is $\text{#}\mathcal{G} = \varphi(N)$, and as such we have for any number $a \in \mathcal{G}$, by Euler’s theorem, $a^{\text{#}\mathcal{G}} = a^{\varphi(N)} = 1$. From which we then normally get that $ed = 1 + k\varphi(N)$ and $a^{ed} = 1^k a = a$.
However, if we apply Euler’s theorem and the Chinese Remainder Theorem, we can see that, writing $p - 1$ and $q - 1$ in their prime factorizations, \(\mathcal{G} \cong \prod_{r^e} (\mathbb{Z}/r\mathbb{Z})^e \prod_{s^e} (\mathbb{Z}/s\mathbb{Z})^e\) (note, this only considers the regular case $N = pq$ with $p, q$ prime, the generalization can be considered in a very similar manner).
When we have an $r \ne 1$ that divides both $(p - 1)$ and $(q - 1)$, or alternatively $r \mid \gcd(p - 1, q - 1)$, it will appear as a factor $r^2$ in the value of $\varphi(N)$, but raising an element to the $r$th power will be enough to clear both components of order $r$ in the above decomposition. As such, we know that an exponent of $\frac{\varphi(N)}{r}$ will already suffice to obtain $1$.
Now, since $p$ and $q$ are both odd primes (we exclude the trivial prime 2, which would not help our security in the slightest), we know that both $p - 1$ and $q - 1$ are even and hence $2 \mid \gcd(p - 1, q - 1)$. More generally, if we include all common factors of $p - 1$ and $q - 1$, we get that \(\forall a \in \mathcal{G}. a^{\mathrm{lcm}(p - 1, q - 1)} = 1.\)
And thus, we have arrived at the Carmichael totient, which is the minimal exponent $\lambda(N)$ such that for every element $a \in \mathcal{G}$ we have that $a^{\lambda(N)} = 1 \pmod N$.
This means, for the case $N = pq$, that $\lambda(N) \mid \frac{\varphi(N)}{2}$, and that $ed \equiv 1 \pmod{\lambda(N)}$ is enough to guarantee correct decryption. From these two facts, we can observe that both $d_1 = e^{-1} \pmod{\lambda(N)})$ and $d_2 = d_1 + \lambda(N)$ give us correct decryptions, while fitting the criteria for the challenge.
If we furthermore observe that at most one of $d_1, d_2$ can be equal to $e^{-1} \mod \varphi(N)$, we have found our solution.
To obtain $p$ and $q$ from $(N, e, d)$ there exist clean mathematical approaches, but we can also opt to rely on Pycryptodome’s implementation of this, by leveraging the different number of arguments we can pass to the Crypto.PublicKey.RSA.construct function.
Implementation
The reference solution takes exactly the described approach:
from pwn import *
import ast, math
from Crypto.PublicKey import RSA
if args.LOCAL:
io = process(["python", "rsajam.py"])
else:
io = remote(args.HOST, args.PORT)
io.recvline()
globals().update(ast.literal_eval(io.recvline().decode()))
key = RSA.construct((N, e, d))
p, q = key.p, key.q
lam = (p - 1) * (q - 1) // math.gcd(p - 1, q - 1)
d2 = pow(e, -1, lam)
if d2 == d:
d2 += lam
io.sendline(str(d2))
io.stream()
Flag
CHTB{lambda_but_n0t_lam3_bda}
Super Metroid
Author: Jack
Samus needs our help! After a day of burning out her Arm Cannon, blasting Metroids and melting the Mother Brain, she’s found her ship’s maps have all been encrypted. Lucky for her, these aliens still don’t know what they’re doing and are trying to roll their own crypto. Can you recover the flag from their elliptic protocol?
Challenge
from Crypto.Util.number import bytes_to_long, getPrime
from secrets import FLAG
def gen_key():
from secrets import a,b
E1 = EllipticCurve(F, [a,b])
assert E.is_isomorphic(E1)
key = - F(1728) * F(4*a)^3 / F(E1.discriminant())
return key
def encrypt(message, key):
m = bytes_to_long(message)
e = 0x10001
G = E.lift_x(Integer(m))
P = e*G
return int(P[0])^^int(key)
p = getPrime(256)
F = GF(p)
E = EllipticCurve(F, [1,2])
key = gen_key()
c1 = encrypt(FLAG[:22], 0)
c2 = encrypt(FLAG[22:], key)
print(f'p = {p}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')
Solution
This challenge performs two stages of encryption:
- RSA-like encryption where $P = [e]G$ where $G$ is a point on an elliptic curve where the x-coordinate a flag fragment
- XOR encryption using a key derived from a second elliptic curve where the parameters of the curve are secret
In RSA, decryption is hard without knowing $\phi(N)$, which allows us to compute $d \equiv e^{-1} \mod \phi(N)$. For this challenge, we are looking for:
\[d = e^{-1} \mod n\]where $n$ is the order of the curve. The order of an elliptic curve is efficently calculated using Schoof’s algorithm. In SageMath we can use this algorithm to find $n$:
F = GF(p)
E = EllipticCurve(F, [1,2])
n = E.order()
Then, just like as in RSA, we can find the inverse of $e$.
Note for beginners: when considering RSA what we really want to do is find $m$ from $c = m^e$. We do this by computing $c^d = m^{de} = m$. This wraps around as the order of the element $m$ is at most $\phi(N)$.
For elliptic curves, our group operation is addition rather than multiplication, and for a point $G$ we know its order is at most $n$. Such that $[n] G = 0$, where $0$ is the identity element of the group operation on the elliptic curve. Think back to RSA again where Euler’s theorem gives us $m^{\phi(N)} \equiv 1 \mod N$ and $1$ is the identity element in $F_N^\star$.
For more details on finite fields and the order of group elements see our blog post.
The second piece of the puzzle is the generation of the key from the function gen_key() which using an unknown curve computes
where we have used the the discriminant of the ellptic curve is gievn by $\Delta = -16(4a^3 + 27b^2)$.
The value $j$ is a very special invariant of an elliptic curve known as the j-invariant and is the same for all curves which are isomorphic to each other. As we know that the secret curve is isomorphic to the given curve, we can compute $j$ from the curve we are given to derive the key. You can read more about the j-invariant if you’re interested.
All that’s left is to implement this in sage and grab the flag.
Implementation
from Crypto.Util.number import long_to_bytes
p = 103286641759600285797850797617629977324547405479993669860676630672349238970323
c1 = 39515350190224022595423324336682561295008443386321945222926612155252852069385
c2 = 102036897442608703406754776248651511553323754723619976410650252804157884591552
F = GF(p)
E = EllipticCurve(F, [1,2])
n = E.order()
d = inverse_mod(0x10001, n)
key = int(E.j_invariant())
P1 = E.lift_x(Integer(c1))
P2 = E.lift_x(Integer(c2^^key))
G1 = d*P1
G2 = d*P2
flag = long_to_bytes(int(G1[0])) + long_to_bytes(int(G2[0]))
print(flag)
# b'CHTB{Counting_points_with_Schoofs_algorithm}'
Flag
CHTB{Counting_points_with_Schoofs_algorithm}
Forge of Empires
Author: Jack
Over thousands of miles, a messenger from the East has arrived with the sacred text. To enable
PHOTON MANand crush the aliens with your robot troopers, the messenger needs you to sign your message!
Challenge
from random import randint
from math import gcd
from Crypto.Util.number import long_to_bytes, bytes_to_long
def gen_keys():
x = randint(1, p-2)
y = pow(g, x, p)
return (x, y)
def sign(message: str, x: int):
while True:
m = int(message, 16) & MASK
k = randint(2, p-2)
if gcd(k, p - 1) != 1:
continue
r = pow(g, k, p)
s = (m - x*r) * pow(k,-1,p-1) % (p - 1)
if s == 0:
continue
return (r,s)
def verify(message: str, r: int, s: int, y: int):
m = int(message, 16) & MASK
if any([x <= 0 or x >= p-1 for x in [m,r,s]]):
return False
return pow(g, m, p) == (pow(y, r, p) * pow(r, s, p)) % p
def get_flag(message: str, r: int, s: int, y: int):
if b'get_flag' not in bytes.fromhex(message):
return 'Error: message does not request the flag'
elif verify(message, r, s, y):
return FLAG
else:
return 'Error: message does not match given signature'
if __name__ == "__main__":
import os
os.chdir(os.path.abspath(os.path.dirname(__file__)))
with open("flag.txt", 'rb') as f:
FLAG = f.read()
p = 2**1024 + 1657867
g = 3
MASK = (2**p.bit_length() - 1)
x, y = gen_keys()
print(f"Server's public key: {y}")
print(f'Please send your request message and signature (r,s)')
message = input('message: ')
r = int(input('r: '))
s = int(input('s: '))
flag = get_flag(message, r, s, y)
print(flag)
Solution
The intended solution here consists of first generating an existential forgery for the given public key, due to the fact that the message is not being hashed (see e.g. the section on the Wikipedia page), and then hide the flag in there.
The way we can hide the flag in an existential forgery, i.e. a forgery where we normally can’t control the message, is due to another error in the code: MASK is applied when checking the signature, but not when checking the presence of get_flag. This allows us to place get_flag in bits that get masked out.
Alternatively, there was also an unintended solution, due to 3 not being a generator of the entire group, but only half of it. This allows us to find the order of g, y and r, so that we can make the verification perform the comparison $1 \overset{?}{=} 1 \cdot 1$.
Implementation
Note: I was lazy and didn’t make something which connected to the server, I simply copy pasted the output.
from random import randint
from math import gcd
from Crypto.Util.number import long_to_bytes, bytes_to_long
p = 2**1024 + 1657867
MASK = (2**p.bit_length() - 1)
g = 3
def forgery(y: int):
e = randint(1, p-1)
r = y*pow(g,e,p) % p
s = -r % (p - 1)
m = (e*s) % (p-1)
m += (bytes_to_long(b'get_flag') << 1200)
M = hex(m)[2:]
return(M,r,s)
y = int(input('public key: '))
M, r, s = forgery(y)
print(f'M: {M}')
print(f'r: {r}')
print(f's: {s}')
Flag
CHTB{Elgamal_remember_to_hash_your_messages!}
Tetris
Author: Robin
It seems the aliens might be living backwards in time, so now we’re suddenly seeing completely different and older kinds of cipher too.
The flag consists entirely of uppercase characters, and is of the formCHTB{SOMETHINGHERE}. You’ll still have to insert the{}yourself.
Challenge
# The flag consists of only uppercase ascii letters
# You do have to fix up the flag format yourself
import string, hashlib, itertools
def clean(x):
return ''.join(c for c in x.upper() if c in string.ascii_letters)
def transpose(x, l):
return ''.join(x[i::l] for i in range(l))
def alphabet(r):
a = list(string.ascii_uppercase)
for i in range(len(a) - 1, 0, -1):
j = r.randrange(0, i)
a[i], a[j] = a[j], a[i]
return ''.join(a)
def encrypt(text, l, key):
enc = text.translate(''.maketrans(string.ascii_uppercase, key))
return transpose(enc, l)
class RNG:
A = 101565695086122187
C = 56502943171806276
M = 288230376151711717
def __init__(self, seed):
self.state = seed
def next(self):
self.state = ((self.state * self.A) + self.C) % self.M
return self.state
def randrange(self, low, high):
assert high > low
range = high - low
limit = range * (self.M // range)
while True:
res = self.next()
if res <= limit:
return (res % range) + low
if __name__ == "__main__":
with open("content.txt", "r") as f:
text = clean(f.read())
with open("flag.txt", "r") as f:
text += clean(f.read())
seed = int.from_bytes(hashlib.sha256(text.encode()).digest(), "big")
rng = RNG(seed)
L = rng.randrange(1, 100)
print(f"{L = }")
key = alphabet(rng)
with open("content.enc.txt", "w") as f:
f.write(encrypt(text, L, key))
Solution
We see a bit of classical crypto this time, where we get the source code for once, so hopefully not something where we just need to guess the cryptosystem used and throw some classical online solver at it.
Analyzing it further, and ignoring the custom PRNG as we can’t see an immediate attack on it, we observe that the encryption happens in two steps. First, a monoalphabetic substitution with a random key is applied, then an unkeyed transposition of some unknown length $L$ happens.
Finding L
$L$ comes from a limited range, so if we can have an efficient enough approach to crack the substitution, we could just try all possible $L$ and output the resulting plaintext that scores best (according to some metric discussed below).
Scoring plaintext
One often-used approach to determine how close something is to text in a natural language is the Index of Coincidence.
Every language has a more or less known and unique IoC, so by comparing the IoC of a piece of text to reference IoCs, we can try to identify if this is a text in a given language.
Interestingly, this metric is invariant under monoalphabetic substitution and reordering, so while in other cases this can give us some much needed extra flexibility and power, in this case it is not enough to determine $L$ directly, as any choice of $L$ would give the same IoC value.
Finding L (reprise)
Now, rather than trying to decrypt the substitution for every possible $L$, we could also consider a scoring based on bigram IoC, which would no longer be invariant under transposition, and should allow us to accurately detect the correct $L$.
Following that, we could then even fall back on the wonderful quipqiup to solve the substition for us. The reference solution however takes the former approach, as we’ll use something extending this solving technique for the followup challenge Tetris 3D.
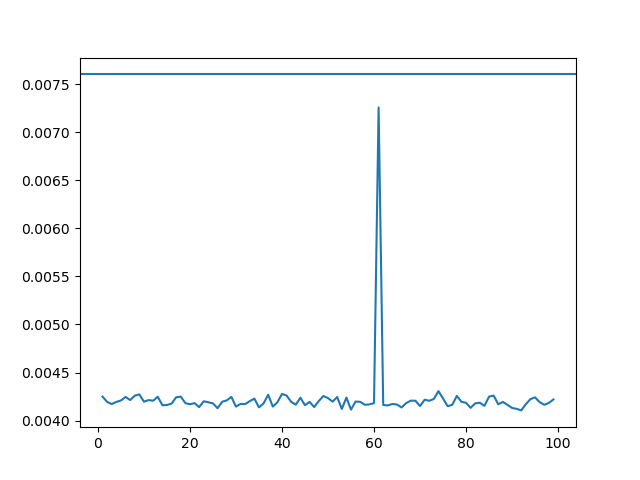
A quick implementation can still clearly convince us of the right value of $L$ however:
Solving substitutions
After our discussion of the IoC, which can be considered as a summarizing metric of the character distribution of a piece of text, we now remark that the distribution over quadgrams of a piece of text is usually very accurate in characterizing that text. Be it based on the language used, or even the author or the style of the text itself.
In this case, we will assume we have a correctly untransposed piece of text, that is as such a simple monoalphabetic substitution.
Our general approach will be one of Hill Climbing. That is, we will start off with a completely random alphabet key, and mutate it iteratively such that it maximally improves a fitness score.
For us, this fitness score will be then based on some reference quadgram statistics.
We could attempt to write a clever fitness function for this based on e.g. the chi-squared test, but simply taking a sum in log-space with an aptly chosen fallback for “impossible” quadgrams gives us generally good results.
Implementation
To derive the theoretical/reference values for both the quadgram statistics of english text, we use a text version of Dickens’ “A Tale of Two Cities”, downloaded from Project Gutenberg.
from collections import Counter
import string, itertools, math
def clean(x):
return ''.join(c for c in x.upper() if c in string.ascii_letters)
def untranspose(c, l):
n = len(c) // l
r = []
s = 0
for i in range(l):
t = n
if len(c) % l > i:
t = n + 1
r.append(c[s:s+t])
s += t
res = ''.join(''.join(p) for p in itertools.zip_longest(*r, fillvalue=''))
assert c == ''.join(res[i::l] for i in range(l))
return res
def quadgramstats(x):
c = Counter(x[i:i+4] for i in range(len(x) - 4))
return {k:math.log(v / len(x), 10) for k, v in c.most_common()}
def score(x):
return sum(targetQuad.get(x[i:i+4], -24) for i in range(len(x) - 4)) / (len(x) - 3)
def fullscore(x, key):
return score(x.translate(''.maketrans(string.ascii_uppercase, key)))
def swap(x, a, b):
assert a <= b
if a == b: return x
return x[:a] + x[b] + x[a+1:b] + x[a] + x[b+1:]
def hillclimb(c):
key = string.ascii_uppercase
target = fullscore(c, key)
change = True
while change:
change = False
for a in range(1, 26):
for b in range(a):
t = swap(key, b, a)
ts = fullscore(c, t)
if ts > target:
target = ts
change = True
key = t
return key
reference = clean(open("atotc.txt", "r").read())
targetQuad = quadgramstats(reference)
ctxt = clean(open("content.enc.txt", "r").read())
best = None
bb = -float("inf")
bl = -1
for L in range(1, 100):
t = untranspose(ctxt, L)
key = hillclimb(t)
p = t.translate(''.maketrans(string.ascii_uppercase, key))
bb, bl, best = max((bb, bl, best), (s := score(p), L, p))
print(L, "=>", s)
print(bb, bl, best)
And we also provide the alternative script to find the correct value of $L$ based on bigram IoC:
from matplotlib import pyplot as plt
from collections import Counter
import string, itertools
def clean(x):
return ''.join(c for c in x.upper() if c in string.ascii_letters)
def IoC(x):
num = sum(x * (x - 1) for _, x in Counter(x).most_common())
den = len(x) * (len(x) - 1)
return num / den
def bigrams(x):
return [x[i:i+2] for i in range(len(x) - 1)]
def untranspose(c, l):
n = len(c) // l
r = []
s = 0
for i in range(l):
t = n
if len(c) % l > i:
t = n + 1
r.append(c[s:s+t])
s += t
res = ''.join(''.join(p) for p in itertools.zip_longest(*r, fillvalue=''))
assert c == ''.join(res[i::l] for i in range(l))
return res
reference = clean(open("atotc.txt", "r").read())
ctxt = clean(open("content.enc.txt", "r").read())
points = [IoC(bigrams(untranspose(ctxt, L))) for L in range(1, 100)]
plt.plot(range(1, 100), points)
plt.axhline(y = IoC(bigrams(reference)))
# plt.show()
plt.savefig("plot_L.png")
print(f"L = {max(range(1, 100), key=lambda i: points[i - 1])}")
Flag
CHTB{UNFORTUNATELYQUIPQIUPDOESNTSUPPORTTRANSPOSITIONS}
Little Nightmares
Author: Jack
Never in your darkest moments did your childhood fears prepare you for an alien invasion. To make matters worse, you’ve just been given a Little homework by the Lady. Defeat this and she will retreat into the night.
Challenge
from Crypto.Util.number import getPrime, bytes_to_long
from random import randint
FLAG = b'CHTB{??????????????????????????????????}'
flag = bytes_to_long(FLAG)
def keygen():
p, q = getPrime(1024), getPrime(1024)
N = p*q
g, r1, r2 = [randint(1,N) for _ in range(3)]
g1, g2 = pow(g, r1*(p-1), N), pow(g, r2*(q-1), N)
return [N, g1, g2], [p, q]
def encrypt(m, public):
N, g1, g2 = public
assert m < N, "Message is too long"
s1, s2 = randint(1,N), randint(1,N)
c1 = m*pow(g1,s1,N) % N
c2 = m*pow(g2,s2,N) % N
return [c1, c2]
def decrypt(enc, private):
c1, c2 = enc
p, q = private
m1 = c1 * pow(q, -1, p) * q
m2 = c2 * pow(p, -1, q) * p
return (m1 + m2) % (p*q)
public, private = keygen()
enc = encrypt(flag, public)
assert flag == decrypt(enc, private)
print(f'Public key: {public}')
print(f'Encrypted Flag: {enc}')
Solution
This challenge was inspired by a homework question I helped a friend with which was based on the same cryptosystem. The cryptosystem is as follows.
Two large primes $p$ and $q$ are picked an a public modulus $N = pq$ is formed. Three random integers in $\mathbb{F}_N^\star$: $(g,r_1,r_2)$ are picked and then the public key:
\[N, \quad g_1 = g^{r_1(p-1)} \pmod N, \quad g_2 = g^{r_2(q-1)} \pmod N\]is computed. The private key is $p,q$.
To solve this puzzle, we then need to find the private key given only the public key. As this is possible, we see this cryptosystem is totally broken and not secure at all!
We give you the decrypt function, so all we need to do is factor $N$.
To do this, we notice that
\[g_1 \equiv 1 \pmod p, \qquad g_2 \equiv 1 \pmod q\]due to Fermat’s little theorem that
\[g^{p-1} \equiv 1 \pmod p \;\; \Rightarrow \;\; g^{r_1(p-1)} \equiv 1^{r_1} \equiv 1 \pmod p\]Without taking the modulus, we can write $g_1$ as:
\[g_1 = g^{r_1(p-1)} = 1 + kp\]for some integer $k$ and looking at this modulo the public key we have:
\[g_1 \mod N = 1 + k p - \ell N\]for some integers $(k, \ell)$. We can do a bit of algebra to show:
\[g_1 \mod N = 1 + k p - \ell N = 1 + p(k + \ell q)\]and from this find $p$ from
\[\gcd(N, g_1 - 1) = \gcd(pq, p(k + \ell q)) = p\]We note you can do exactly the same with $g_2$ and $q$, or simply find $q$ from $q = N / p$.
Implementation
from Crypto.Util.number import long_to_bytes
from functools import reduce
import math
public = [15046368688522729878837364795846944447584249939940259042809310309990644722874686184397211078874301515249887625469482926118729767921165680434919436001251916009731653621249173925306213496143518405636216886510423114656445458948673083827223571060637952939874530020017901480576002182201895448100262702822444377134178804257755785230586532510071013644046338971791975792507111644403115625869332161597091770842097004583717690548871004494047953982837491656373096470967389016252220593050830165369469758747361848151735684518721718721910577759955840675047364431973099362772693817698643582567162750607561757926413317531802354973847, 9283319553892803764690461243901070663222428323113425322850741756254277368036028273335428365663191030757323877453365465554132886645468588395631445445583253155195968694862787593653053769030730815589172570039269584478526982112345274390480983685543611640614764128042195018064671336591349166188571572536295612195292864841173479903528383123563226015278849646883506520514470333897880659139687610612049230856991239192330160727258048546502899802982277188877310126410571180236389500463464659397850999622904270520629126455639717497594792781963273264274684421455422023088932590387852813426966580288533263121276557350436900246463, 8170671201621857973407215819397012803619280999847588732628253232283307833188933536560440103969432332185848983745037071025860497584949115721267685519443159539783527315198992420655868110884873218133385835580345201078361745220227561551654718787264374257293351098299807821798471006283753277157555438331734456302990269860368479905882644912688806233577606978042582643369428542665819950283055672363935065844777322370865181261974289403517780920801228770368401030437376412993457855872519154731210534206120823952983817295670102327952847504357905927290367724038039202573992755780477507837498958878434898475866081720566629437645]
enc = [7276931928429452854246342065839521806420418866856294154132077445353136752229297971239711445722522895365037966326373464771601590080627182837712349184127450287007143044916049997542062388957038193775059765336324946772584345217059576295657932746876343366393024413356918508539249571136028895868283293788299191933766033783323506852233709102246103073938749386863417754855718482717665887208176012160888333043927323096890710493237011980243014972091979988123240671317403963855512078171350546136813316974298786004332694857700545913951953794486310691251777765023941312078456072442404873687449493571576308437181236785086220324920, 323136689475858283788435297190415326629231841782013470380328322062914421821417044602586721782266492137206976604934554032410738337998164019339195282867579270570771188637636630571301963569622900241602213161396475522976801562853960864577088622021373828937295792222819561111043573007672396987476784672948287600574705736056566374617963948347878220280909003723932805632146024848076789866573232781595349191010186788284504514925388452232227920241883518851862145988532377145521056940790582807479213216240632647108768886842632170415653038740093542869598364804101879631033516030858720540787637217275393603575250765731822252109]
def decrypt(enc, private):
sum = 0
prod = reduce(lambda a, b: a*b, private)
for a_i, n_i in zip(enc, private):
p = prod // n_i
sum += a_i * pow(p, -1, n_i) * p
return sum % prod
N, g1, g2 = public
p = math.gcd(g1 - 1, N)
q = math.gcd(g2 - 1, N)
f = decrypt(enc, [p,1])
print(long_to_bytes(f))
#b'CHTB{Factoring_With_Fermats_Little_Theorem}''
Flag
CHTB{Factoring_With_Fermats_Little_Theorem}
Hard
Wii Phit
Author: Jack
The aliens have encrypted our save file from Wii Phit and we’re about to lose our 4,869 day streak!! They’re even taunting us with a hint. I think the alien’s are getting a bit over-confident if you ask me.
Challenge
from Crypto.Util.number import bytes_to_long
from secrets import FLAG,p,q
N = p**3 * q
e = 0x10001
c = pow(bytes_to_long(FLAG),e,N)
print(f'Flag: {hex(c)}')
# Hint
w = 25965460884749769384351428855708318685345170011800821829011862918688758545847199832834284337871947234627057905530743956554688825819477516944610078633662855
x = p + 1328
y = p + 1329
z = q - 1
assert w*(x*z + y*z - x*y) == 4*x*y*z
Intended Solution
This challenge is a straightforward RSA one where the factors of the RSA modulus are found by solving the equation
\[w (xz + yz - xy) = 4 xyz\]Where the only known value is $w$ and $(x,y,z)$ are related to the prime factors of the modulus: $N = p^3 q$.
Rearrange the above equation, we obtain
\[\frac{4}{w} = \frac{1}{x} + \frac{1}{y} - \frac{1}{z}\]This is a well known Diophantine equation related to the Erdős–Straus conjecture which states that for $n \geq 2$ there is a solution of the equation
\[\frac{4}{w} = \frac{1}{x} + \frac{1}{y} + \frac{1}{z}\]for positive integers $(x,y,z)$.
The equation presented in this challenge is a little easier as the last term is negative. Using that $w$ is odd, we can write
\[\frac{4}{w} = \frac{2}{w-1} + \frac{2}{w+1} - \frac{4}{w(w-1)(w+1)}\]We can simplify this a little using that $w = 2k + 1$ such that
\[\frac{4}{w} = \frac{1}{k} + \frac{1}{k+1} - \frac{1}{k (k + 1) (2k + 1)}\]From the above relations we have that:
\[\begin{aligned} w &= 2k + 1, \\ x &= k, \quad y = k + 1, \quad z= k (k + 1) (2k + 1)\\ x &= p + 1328, \quad y = p + 1329, \quad z = q - 1 \end{aligned}\]So we can simply solve for our two primes with
\[k = \frac{w-1}{2}, \quad p = k - 1328, \quad q = k (k + 1) (2k + 1) + 1\]Below we implement this in python and solve for the flag.
Note for beginners to compute the private exponent $d = e^{-1} \mod \phi(N)$ we need to compute the totient of the public modulus. This is
\[\phi(N) = p^2 (p-1)(q-1),\]where we have used that:
\[\phi(xy) = \phi(x)\phi(y), \qquad \phi(p^k) = p^{k-1} (p - 1)\]for all co-prime integers $(x,y)$ and all primes $p$. Note that this is different from textbook RSA where:
\[N = pq, \qquad \phi(N) = (p-1)(q-1).\]Implementation
from Crypto.Util.number import long_to_bytes
# Challenge Data
c = 0x12f47f77c4b5a72a0d14a066fedc80ba6064058c900a798f1658de60f13e1d8f21106654c4aac740fd5e2d7cf62f0d3284c2686d2aac261e35576df989185fee449c20efa171ff3d168a04bce84e51af255383a59ed42583e93481cbfb24fddda16e0a767bff622a4753e1a5df248af14c9ad50f842be47ebb930604becfd4af04d21c0b2248a16cdee16a04b4a12ac7e2161cb63e2d86999a1a8ed2a8faeb4f4986c2a3fbd5916effb1d9f3f04e330fdd8179ea6952b14f758d385c4bc9c5ae30f516c17b23c7c6b9dbe40e16e90d8734baeb69fed12149174b22add6b96750e4416ca7addf70bcec9210b967991e487a4542899dde3abf3a91bbbaeffae67831c46c2238e6e5f4d8004543247fae7ff25bbb01a1ab3196d8a9cfd693096aabec46c2095f2a82a408f688bbedddc407b328d4ea5394348285f48afeaafacc333cff3822e791b9940121b73f4e31c93c6b72ba3ede7bba87419b154dc6099ec95f56ed74fb5c55d9d8b3b8c0fc7de99f344beb118ac3d4333eb692710eaa7fd22
e = 0x10001
w = 25965460884749769384351428855708318685345170011800821829011862918688758545847199832834284337871947234627057905530743956554688825819477516944610078633662855
# Deriving p,q
k = (w - 1) // 2
p = k - 1328
q = k*(k+1)*(2*k+1) + 1
# Solve
N = p**3 * q
phi = p**2*(p-1)*(q-1)
d = pow(e,-1,phi)
m = pow(c,d,N)
print(long_to_bytes(m))
# b'CHTB{Erdos-Straus-Conjecture}'
Flag
CHTB{Erdos-Straus-Conjecture}
Unintended Solution or How z3 is Magic
During the CTF we heard from a few players who solved this challenge by using the z3-solver package. When I made this challenge, I assumed the size of w would make this impossible in a reasonable amount of time, but I was wrong!
During playtesting, Robin tried solving this with z3 and found that the code hung. The crucial piece that we missed during playtesting was to constrain p,q > 0. Removing this condition from the below code, z3 doesnt seem to be able to find the primes. Thanks to unblvr and killerdog who both messaged us about this solution.
Unintended Implementation or All hail z3
from z3 import *
from Crypto.Util.number import long_to_bytes
c = 0x12f47f77c4b5a72a0d14a066fedc80ba6064058c900a798f1658de60f13e1d8f21106654c4aac740fd5e2d7cf62f0d3284c2686d2aac261e35576df989185fee449c20efa171ff3d168a04bce84e51af255383a59ed42583e93481cbfb24fddda16e0a767bff622a4753e1a5df248af14c9ad50f842be47ebb930604becfd4af04d21c0b2248a16cdee16a04b4a12ac7e2161cb63e2d86999a1a8ed2a8faeb4f4986c2a3fbd5916effb1d9f3f04e330fdd8179ea6952b14f758d385c4bc9c5ae30f516c17b23c7c6b9dbe40e16e90d8734baeb69fed12149174b22add6b96750e4416ca7addf70bcec9210b967991e487a4542899dde3abf3a91bbbaeffae67831c46c2238e6e5f4d8004543247fae7ff25bbb01a1ab3196d8a9cfd693096aabec46c2095f2a82a408f688bbedddc407b328d4ea5394348285f48afeaafacc333cff3822e791b9940121b73f4e31c93c6b72ba3ede7bba87419b154dc6099ec95f56ed74fb5c55d9d8b3b8c0fc7de99f344beb118ac3d4333eb692710eaa7fd22
e = 0x10001
w = 25965460884749769384351428855708318685345170011800821829011862918688758545847199832834284337871947234627057905530743956554688825819477516944610078633662855
p = Int("p")
q = Int("q")
x = p + 1328
y = p + 1329
z = q - 1
s = Solver()
s.add(p>0)
s.add(q>0)
s.add(w*(x*z + y*z - x*y) == 4*x*y*z)
if s.check() == sat:
m = s.model()
p = m[p].as_long()
q = m[q].as_long()
e = 0x10001
N = p**3 * q
phi = p**2*(p-1)*(q-1)
d = pow(e,-1,phi)
m = pow(c,d,N)
print(long_to_bytes(m))
#b'CHTB{Erdos-Straus-Conjecture}'
This blog post is getting pretty long, so we broke off the last four challenges into their own blog post.