CryptoCTF 2021 - Medium | CryptoHack Blog

Last week, CryptoHackers got together to play CryptoCTF for the second time as a team. We solved 26/29 of the challenges during the 24 hour window and came third overall. First and second places went to Super Guessers (Rkm and Rbtree are very friendly faces from CryptoHack) and a Vietnamese team working together to support the spirit of Ho Chi Minh city and nearby provinces. Congratulations to them both.

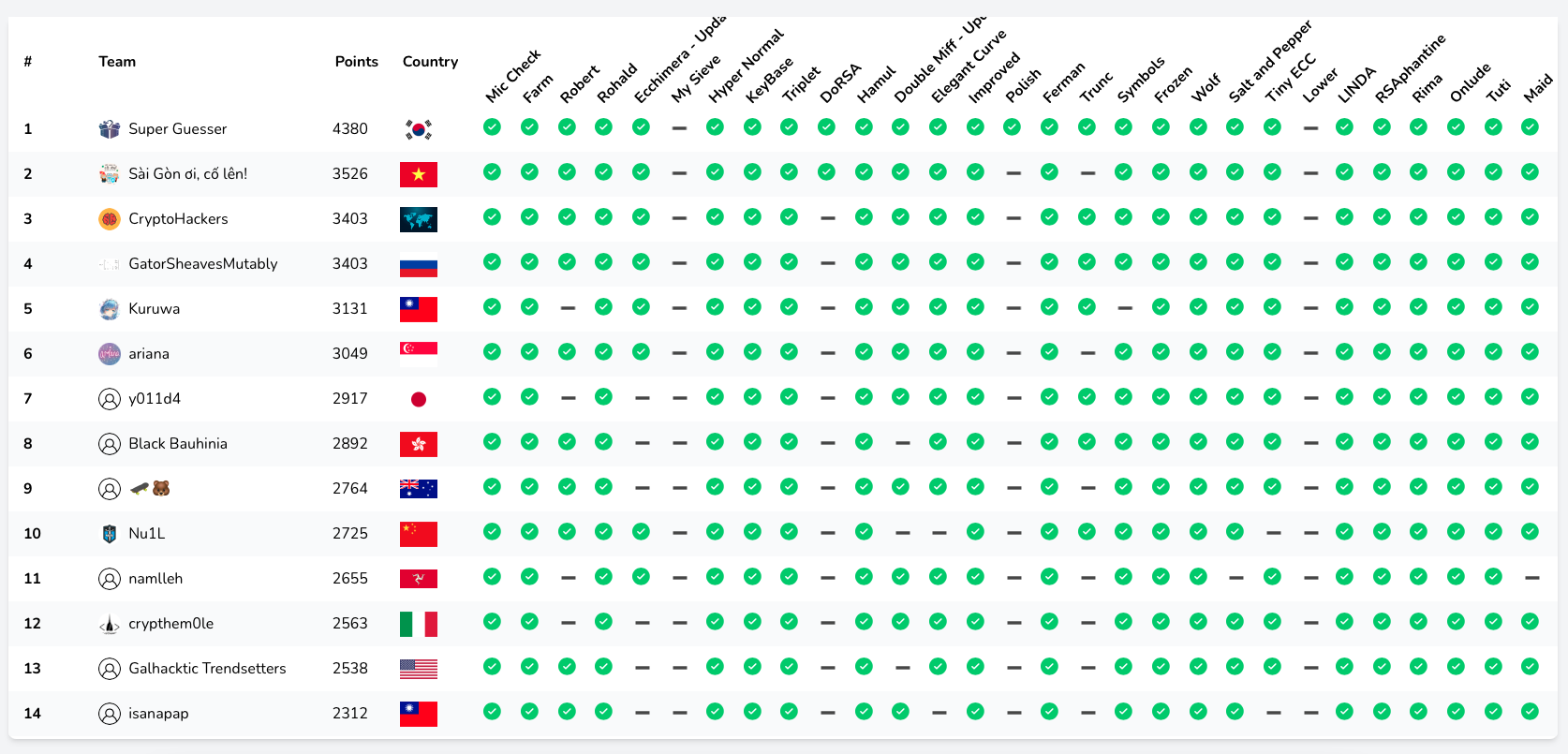
CTF Scoreboard

Not only was it a lot of fun for us all to play together, but it was amazing to see how many CryptoHack friends played the CTF either solo or in small teams and who were able to get a top 15 spot. We’re honoured to have so many talented people in our Discord, chatting with us about maths and cryptography. We even have guest writeups from rkm0959 talking about the solutions of DoRSA and Polish

Here are the write-ups for the middle-difficulty challenges in the CTF. You can find write ups for the easy and hard challenges as other posts on our blog.

Thank you to everyone who played for the CryptoHackers, and to ASIS CTF for organising this enjoyable event. Congratulations again to Super Guessers for being the ultimate crypto heros!

We will be publishing more writeups here as soon as they are finished. If you spot a mistake or an improvement that could be made, please ping jack or hyperreality on CryptoHack Discord.

Challenges

Challenge Name	Category	Solved By	Points
Triplet	RSA	Willwam845, Retroid, Vishiswoz	91
Onlude	Linear algebra	Q7	95
Improved	Asymmetric Collisions	Willwam845, Vishiswoz (Coming Soon)	117
Maid	Rabin Cryptosystem	Defund	119
Wolf	AES-GCM	DD	128
Ferman	Mathematics	Jack	134
RSAphantine	Diophantine Equations	AC, UnblvR, Jack	142
Frozen	Signature Schemes	DD	142
LINDA	Discrete logarithm	NeketmanX	169

Triplet

Challenge

#!/usr/bin/env python3

from Crypto.Util.number import *
from random import randint
import sys
from flag import FLAG

def die(*args):
  pr(*args)
  quit()

def pr(*args):
  s = " ".join(map(str, args))
  sys.stdout.write(s + "\n")
  sys.stdout.flush()

def sc():
  return sys.stdin.readline().strip()

def main():
  border = "+"
  pr(border*72)
  pr(border, " hi talented cryptographers, the mission is to find the three RSA   ", border)
  pr(border, " modulus with the same public and private exponent! Try your chance!", border)
  pr(border*72)

  nbit = 160

  while True:
    pr("| Options: \n|\t[S]end the three nbit prime pairs \n|\t[Q]uit")
    ans = sc().lower()
    order = ['first', 'second', 'third']
    if ans == 's':
      P, N = [], []
      for i in range(3):
        pr("| Send the " + order[i] + " RSA primes such that nbit >= " + str(nbit) + ": p_" + str(i+1) + ", q_" + str(i+1) + " ")
        params = sc()
        try:
          p, q = params.split(',')
          p, q = int(p), int(q)
        except:
          die("| your primes are not valid!!")
        if isPrime(p) and isPrime(q) and len(bin(p)[2:]) >= nbit and len(bin(q)[2:]) >= nbit:
          P.append((p, q))
          n = p * q
          N.append(n)
        else:
          die("| your input is not desired prime, Bye!")
      if len(set(N)) == 3:
        pr("| Send the public and private exponent: e, d ")
        params = sc()
        try:
          e, d = params.split(',')
          e, d = int(e), int(d)
        except:
          die("| your parameters are not valid!! Bye!!!")
        phi_1 = (P[0][0] - 1)*(P[0][1] - 1)
        phi_2 = (P[1][0] - 1)*(P[1][1] - 1)
        phi_3 = (P[2][0] - 1)*(P[2][1] - 1)
        if 1 < e < min([phi_1, phi_2, phi_3]) and 1 < d < min([phi_1, phi_2, phi_3]):
          b = (e * d % phi_1 == 1) and (e * d % phi_2 == 1) and (e * d % phi_3 == 1)
          if b:
            die("| You got the flag:", FLAG)
          else:
            die("| invalid exponents, bye!!!")
        else:
          die("| the exponents are too small or too large!")
      else:
        die("| kidding me?!!, bye!")
    elif ans == 'q':
      die("Quitting ...")
    else:
      die("Bye ...")

if __name__ == '__main__':
  main()

We need to send 3 pairs of primes followed by a keypair e,d so that e,d is a valid keypair for each modulus generated by each pair.

Most easy solutions are patched out, as e and d both have to be less than the lowest phi and greater than 1.

Solution

Our main idea for this problem is to generate phi_1, phi_2 and phi_3 in a way so that phi_2 is a multiple of phi_1, and phi_3 is a multiple of phi_2. In this way, any valid keypair for phi_3 (that also satisfies the length requirement) will also be a valid keypair for phi_1 and phi_2 and can be used to get the flag.

We can generate primes as follows:

def phi(p,q):
    return (p-1) * (q-1)

from random import randrange

def genprime(baseprime):
    while True:
        k = randrange(2, 1000)
        p = baseprime * k + 1
        if is_prime(p):
            return p

p = random_prime(2^160)
q = random_prime(2^160)
r = genprime(p)
s = genprime(q)
t = genprime(r)
u = genprime(s)
phi_1 = phi(p,q)
phi_2 = phi(r,s)
phi_3 = phi(t,u)

Now all we need to do is generate a valid keypair for phi_3. To do this, recall that the values $e$ and $d$ satisfy the following equation:

\[e * d \equiv 1 \mod \phi(n)\]

therefore

\[e * d = 1 + k * \phi(n)\]

If we find factors of $1 + phi(n3)$, we should be able to find two numbers that are small enough to satisfy the length requirements, as the value $k$ in the equation

\[\phi(n3) = k * \phi(n1)\]

should be small. We can just use something like factordb for this.

Once we do that, we submit everything to the server and get our flag.

Example input:

1016528131013635090619361217720494946552931485213,1429584882448210886669728733194710184148915763157
6211546314237476302579971345731015750127038990912821,8860059189914843449838352373651833954155350825107793
9404281119755539122106076617436757845692337032242009481,24063920759808714809760965046838381019485932840992763073
43589288709210633359625764026901174390804401096987086682930362519465081895858044399533,5191731325979249818708517

Flag

CCTF{7HrE3_b4Bie5_c4rRi3d_dUr1nG_0Ne_pr39naNcY_Ar3_triplets}

Onlude

Challenge

Encryption and Decryption could be really easy, while we expected the decryption to be harder!

#!/usr/bin/env sage

from sage.all import *
from flag import flag

global p, alphabet
p = 71
alphabet = '=0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ$!?_{}<>'

flag = flag.lstrip('CCTF{').rstrip('}')
assert len(flag) == 24

def cross(m):
    return alphabet.index(m)

def prepare(msg):
    A = zero_matrix(GF(p), 11, 11)
    for k in range(len(msg)):
        i, j = 5*k // 11, 5*k % 11
        A[i, j] = cross(msg[k])
    return A

def keygen():
    R = random_matrix(GF(p), 11, 11)
    while True:
        S = random_matrix(GF(p), 11, 11)
        if S.rank() == 11:
            _, L, U = S.LU()
            return R, L, U

def encrypt(A, key):
    R, L, U = key
    S = L * U
    X = A + R
    Y = S * X
    E = L.inverse() * Y
    return E

A = prepare(flag)
key = keygen()
R, L, U = key
S = L * U
E = encrypt(A, key)
print(f'E = \n{E}')
print(f'L * U * L = \n{L * U * L}')
print(f'L^(-1) * S^2 * L = \n{L.inverse() * S**2 * L}')
print(f'R^(-1) * S^8 = \n{R.inverse() * S**8}')

E = 
[25 55 61 28 11 46 19 50 37  5 21]
[20 57 39  9 25 37 63 31 70 15 47]
[56 31  1  1 50 67 38 14 42 46 14]
[42 54 38 22 19 55  7 18 45 53 39]
[55 26 42 15 48  6 24  4 17 60 64]
[ 1 38 50 10 19 57 26 48  6  4 14]
[13  4 38 54 23 34 54 42 15 56 29]
[26 66  8 48  6 70 44  8 67 68 65]
[56 67 49 61 18 34 53 21  7 48 32]
[15 70 10 34  1 57 70 27 12 33 46]
[25 29 20 21 30 55 63 49 11 36  7]
L * U * L = 
[50  8 21 16 13 33  2 12 35 20 14]
[36 55 36 34 27 28 23 21 62 17  8]
[56 26 49 39 43 30 35 46  0 58 43]
[11 25 25 35 29  0 22 38 53 51 58]
[34 14 69 68  5 32 27  4 27 62 15]
[46 49 36 42 26 12 28 60 54 66 23]
[69 55 30 65 56 13 14 36 26 46 48]
[25 48 16 20 34 57 64 62 61 25 62]
[68 39 11 40 25 11  7 40 24 43 65]
[54 20 40 59 52 60 37 14 32 44  4]
[45 20  7 26 45 45 50 17 41 59 50]
L^(-1) * S^2 * L = 
[34 12 70 21 36  2  2 43  7 14  2]
[ 1 54 59 12 64 35  9  7 49 11 49]
[69 14 10 19 16 27 11  9 26 10 45]
[70 17 41 13 35 58 19 29 70  5 30]
[68 69 67 37 63 69 15 64 66 28 26]
[18 29 64 38 63 67 15 27 64  6 26]
[ 0 12 40 41 48 30 46 52 39 48 58]
[22  3 28 35 55 30 15 17 22 49 55]
[50 55 55 61 45 23 24 32 10 59 69]
[27 21 68 56 67 49 64 53 42 46 14]
[42 66 16 29 42 42 23 49 43  3 23]
R^(-1) * S^8 = 
[51  9 22 61 63 14  2  4 18 18 23]
[33 53 31 31 62 21 66  7 66 68  7]
[59 19 32 21 13 34 16 43 49 25  7]
[44 37  4 29 70 50 46 39 55  4 65]
[29 63 29 43 47 28 40 33  0 62  8]
[45 62 36 68 10 66 26 48 10  6 61]
[43 30 25 18 23 38 61  0 52 46 35]
[ 3 40  6 45 20 55 35 67 25 14 63]
[15 30 61 66 25 33 14 20 60 50 50]
[29 15 53 22 55 64 69 56 44 40  8]
[28 40 69 60 28 41  9 14 29  4 29]

Solution

In this challenge, we are given the source code of an encryption scheme that uses matrix operations for encryption and decryption, the corresponding encrypted flag and some hints.

For the encryption part:

\[E = L^{-1}Y = L^{-1}SX = L^{-1}LU(A+R) = U(A+R)\]

The three hints we have is $LUL$, $L^{-1}S^2L$ and $R^{-1}S^8$

Since $S=LU$, we can rewrite the second hint as $ULUL$, then we can get $U$ by dividing hint1. For the third hint $R^{-1}S^8$, we can rewrite it as $R^{-1}(LULU)^4=R^{-1}(h_1U)^4$, then we can get $R$.

With $U$ and $R$ known, we can then recover the flag $A$ from $E$.

from sage.all import *

E = Matrix(GF(71),[[25,55,61,28,11,46,19,50,37,5,21],
[20,57,39,9,25,37,63,31,70,15,47],
[56,31,1,1,50,67,38,14,42,46,14],
[42,54,38,22,19,55,7,18,45,53,39],
[55,26,42,15,48,6,24,4,17,60,64],
[1,38,50,10,19,57,26,48,6,4,14],
[13,4,38,54,23,34,54,42,15,56,29],
[26,66,8,48,6,70,44,8,67,68,65],
[56,67,49,61,18,34,53,21,7,48,32],
[15,70,10,34,1,57,70,27,12,33,46],
[25,29,20,21,30,55,63,49,11,36,7]])

hint1 = Matrix(GF(71),[[50,8,21,16,13,33,2,12,35,20,14],
[36,55,36,34,27,28,23,21,62,17,8],
[56,26,49,39,43,30,35,46,0,58,43],
[11,25,25,35,29,0,22,38,53,51,58],
[34,14,69,68,5,32,27,4,27,62,15],
[46,49,36,42,26,12,28,60,54,66,23],
[69,55,30,65,56,13,14,36,26,46,48],
[25,48,16,20,34,57,64,62,61,25,62],
[68,39,11,40,25,11,7,40,24,43,65],
[54,20,40,59,52,60,37,14,32,44,4],
[45,20,7,26,45,45,50,17,41,59,50]])

hint2=Matrix(GF(71),[[34,12,70,21,36,2,2,43,7,14,2],
[1,54,59,12,64,35,9,7,49,11,49],
[69,14,10,19,16,27,11,9,26,10,45],
[70,17,41,13,35,58,19,29,70,5,30],
[68,69,67,37,63,69,15,64,66,28,26],
[18,29,64,38,63,67,15,27,64,6,26],
[0,12,40,41,48,30,46,52,39,48,58],
[22,3,28,35,55,30,15,17,22,49,55],
[50,55,55,61,45,23,24,32,10,59,69],
[27,21,68,56,67,49,64,53,42,46,14],
[42,66,16,29,42,42,23,49,43,3,23]])

hint3=Matrix(GF(71),[[51,9,22,61,63,14,2,4,18,18,23],
[33,53,31,31,62,21,66,7,66,68,7],
[59,19,32,21,13,34,16,43,49,25,7],
[44,37,4,29,70,50,46,39,55,4,65],
[29,63,29,43,47,28,40,33,0,62,8],
[45,62,36,68,10,66,26,48,10,6,61],
[43,30,25,18,23,38,61,0,52,46,35],
[3,40,6,45,20,55,35,67,25,14,63],
[15,30,61,66,25,33,14,20,60,50,50],
[29,15,53,22,55,64,69,56,44,40,8],
[28,40,69,60,28,41,9,14,29,4,29]])

U = hint2/hint1
R = (hint3/U/hint1/U/hint1/U/hint1/U/hint1).inverse()
A = U.inverse()*E-R
alphabet = '=0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ$!?_{}<>'
flag = ''
for k in range(24):
    i, j = 5*k // 11, 5*k % 11
    flag+=alphabet[A[i, j]]
print('CCTF{'+flag+'}')

Flag

CCTF{LU__D3c0mpO517Ion__4L90?}

Improved

Coming Soon

Maid

Challenge

#!/usr/bin/python3

from Crypto.Util.number import *
from gmpy2 import *
from secret import *
from flag import flag

global nbit
nbit = 1024

def keygen(nbit):
    while True:
        p, q = [getStrongPrime(nbit) for _ in '01']
        if p % 4 == q % 4 == 3:
            return (p**2)*q, p

def encrypt(m, pubkey):
    if GCD(m, pubkey) != 1 or m >= 2**(2*nbit - 2):
        return None
    return pow(m, 2, pubkey)

def flag_encrypt(flag, p, q):
    m = bytes_to_long(flag)
    assert m < p * q
    return pow(m, 65537, p * q)

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, "  hi all, welcome to Rooney Oracle, you can encrypt and decrypt any ", border)
    pr(border, "  message in this oracle, but the flag is still encrypted, Rooney   ", border)
    pr(border, "  asked me to find the encrypted flag, I'm trying now, please help! ", border)
    pr(border*72)

    pubkey, privkey = keygen(nbit)
    p, q = privkey, pubkey // (privkey ** 2)

    while True:
        pr("| Options: \n|\t[E]ncrypt message \n|\t[D]ecrypt ciphertext \n|\t[S]how encrypted flag \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 'e':
            pr("| Send the message to encrypt: ")
            msg = sc()
            try:
                msg = int(msg)
            except:
                die("| your message is not integer!!")
            pr(f"| encrypt(msg, pubkey) = {encrypt(msg, pubkey)} ")
        elif ans == 'd':
            pr("| Send the ciphertext to decrypt: ")
            enc = sc()
            try:
                enc = int(enc)
            except:
                die("| your message is not integer!!")
            pr(f"| decrypt(enc, privkey) = {decrypt(enc, privkey)} ")
        elif ans == 's':
            pr(f'| enc = {flag_encrypt(flag, p, q)}')
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

We are given access to an oracle which allows us to encrypt and decrypt data with

\[c = m^2 \pmod n, \qquad n = p^2 q\]

and we can request a flag encrypted as

\[c = m^{e} \pmod {pq}, \qquad e = 65537\]

Where $p,q$ are 1024 bit primes. The goal is to use the oracle to factor $n$ and hence obtain the flag.

Solution

The first step is to obtain $n = p^2 q$, which we can do by computing:

\[n = \gcd(m_1^2 - c_1, m^2_2 - c_2)\]

by using the oracle to obtain $c_i$ from integers $m_i$.

Note: there may by other factors, and we actually compute $kn$ for some $k \in \mathbb{Z}$. We can ensure $k = 1$ by computing many $m_i,c_i$ and taking the gcd many times.

The second step is to obtain one of the prime factors.

We cannot send very large numbers to encrypt, but can get around this by sending $E(-X)$ for arbitary sized $X$. As the encryption is simply squaring, this makes no difference. Defund noticed that if you decrypt $X = D(2)$ and then compute $E(-X)$, you do not obtain $2$, but rather some very large integer.

I’m not sure how Defund solved it, but playing with the numbers while writing it up, I noticed that:

\[\gcd(n, D(-1) - 1) = p\]

which allowed me to solve. Looking around online, some other people seem to have solved by doing something like

\[\gcd(n, D(m)^2 - m ) = p^2\]

but seeing as we have no source, a bit of guess work needed to be done one way or another, which seems like a shame.

Implementation

from pwn import *
from Crypto.Util.number import *
from math import gcd
import random

r = remote('04.cr.yp.toc.tf', 38010)

def encrypt(msg):
    r.recvuntil(b"[Q]uit")
    r.sendline(b"E")
    r.recvuntil(b"encrypt: ")
    r.sendline(str(msg))
    r.recvuntil(b" = ")
    return int(r.recvline().strip())

def decrypt(msg):
    r.recvuntil(b"[Q]uit")
    r.sendline(b"D")
    r.recvuntil(b"decrypt: ")
    r.sendline(str(msg))
    r.recvuntil(b" = ")
    return int(r.recvline().strip())

def get_flag():
    r.recvuntil(b"[Q]uit")
    r.sendline(b"S")
    r.recvuntil(b" = ")
    return int(r.recvline().strip())

def recover_n():
    # Obtain kn
    m = 2**1536 - random.randint(1,2**1000)
    c = encrypt(m)
    n = m**2 - c
    # Remove all factors of two
    while n%2 == 0:
        n = n // 2
    # Compute a few more GCD to remove any other factors.
    for _ in range(10):
        m = 2**1536 - random.randint(1,2**1000)
        c = encrypt(m)
        n = gcd(n, m**2 - c)
    return n

def dec_flag(p,q):
    c = get_flag()
    d = pow(0x10001, -1, (p-1)*(q-1))
    m = pow(c,d,p*q)
    return long_to_bytes(m)

def recover_factors(n):
    X = decrypt(-1)
    p = gcd(X - 1, n)
    assert isPrime(p)
    q = n // (p*p) 
    assert isPrime(q)
    return p, q

n = recover_n()
p, q = recover_factors(n)
flag = dec_flag(p,q)
print(flag)
# CCTF{___Ra8!N_H_Cryp70_5YsT3M___}

Flag

CCTF{___Ra8!N_H_Cryp70_5YsT3M___}

Decryption

At the end of the CTF, Factoreal shared the decrypt function. Seeing this, the methods of solving make sense, but it seems like a shame that this wasn’t included within the challenge

def decrypt(c, privkey):
    m_p = pow(c, (privkey + 1) // 4, privkey)
    i = (c - pow(m_p, 2)) // privkey
    j = i * inverse(2*m_p, privkey) % privkey
    m = m_p + j * privkey
    if 2*m < privkey**2:
        return m
    else:
        return privkey**2 - m

Wolf

Challenge

When we connect to the server, it chooses a random length niv between 1 and 11, and a random nonce of that length. We can request the flag encrypted using AES-GCM with the key HungryTimberWolf and that IV, and ask for the server to encrypt our input with the same parameters.

#!/usr/bin/env python3

from Cryptodome.Cipher import AES
import os, time, sys, random
from flag import flag

passphrase = b'HungryTimberWolf'

def encrypt(msg, passphrase, niv):
    msg_header = 'EPOCH:' + str(int(time.time()))
    msg = msg_header + "\n" + msg + '=' * (15 - len(msg) % 16)
    aes = AES.new(passphrase, AES.MODE_GCM, nonce = niv)
    enc = aes.encrypt_and_digest(msg.encode('utf-8'))[0]
    return enc

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, "  hi wolf hunters, welcome to the most dangerous hunting ground!!   ", border)
    pr(border, "  decrypt the encrypted message and get the flag as a nice prize!   ", border)
    pr(border*72)

    niv = os.urandom(random.randint(1, 11))
    flag_enc = encrypt(flag, passphrase, niv)

    while True:
        pr("| Options: \n|\t[G]et the encrypted flag \n|\t[T]est the encryption \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 'g':
            pr(f'| encrypt(flag) = {flag_enc.hex()}')
        elif ans == 't':
            pr("| Please send your message to encrypt: ")
            msg_inp = sc()
            enc = encrypt(msg_inp, passphrase, niv).hex()
            pr(f'| enc = {enc}')
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

Solution

Since niv is uniformly random, in one out of 11 connections the nonce will only be one byte long. If this happens, we can easily bruteforce the encrypted flag: we already know the key, and can try all 256 nonce values to see if one of them gives a plaintext that looks like a flag.

A quick Python script collects encrypted flags, which we can dump into a single file to process later:

#! /usr/bin/env python
from pwn import *

serv = pwnlib.tubes.remote.remote('01.cr.yp.toc.tf', 27010)
serv.sendline('g')
serv.sendline('q')

for line in serv.recvall().decode('utf-8').split('\n'):
    if 'encrypt(flag)' in line:
        print(line.rstrip().split()[-1])

The solver isn’t much longer:

#! /usr/bin/env python
from Cryptodome.Cipher import AES
import binascii

def trysolve(line):
    for iv in range(256):
        a = AES.new(b'HungryTimberWolf', AES.MODE_GCM, nonce=bytes([iv]))
        flag = a.decrypt(binascii.unhexlify(line))
        if b'CTF' in flag:
            print(flag)

with open('flags.txt', 'r') as f:
    for line in f.readlines():
        if not line.startswith('['):
            trysolve(line.rstrip())

Flag

CCTF{____w0lveS____c4n____be____dan9er0uS____t0____p3oplE____!!!!!!}

Ferman

Challenge

Modern cryptographic algorithms are the theoretical foundations and the core technologies of information security. Should we emphasize more?

nc 07.cr.yp.toc.tf 22010

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+  hi talented participants, welcome to the FERMAN cryptography task!  +
+  Solve the given equations and decrypt the encrypted flag! Enjoy!    +
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

| Parameters generation is a bit time consuming, so please be patient :P
| Options: 
|   [P]rint encrypted flag 
|   [R]eveal the parameters 
|   [Q]uit

P
| encrypt(flag) = 6489656589950752810044571176882070993656025408411955877914111875896024399252967804237101085443293019406006339555779534657926807551928549712558667515175079267695028070934727514846970003337126120540450206565849474378607706030211234939933160392491902242074123763448231072583065175864490510115483208842110529309232348180718641618424365058379284549574700049803925884878710773408472100779358561980206902500388524570616750475958017638946408491011264747032498524679282489181606124604218147

R
    e = 65537
    isPrime(p) = True
    isPrime(q) = True
    n = p * q
    (p - 127)**2 + (q - 184)**2 = 13809252727788824044233595548226590341967726502046327883413398709726819135921363848617960542444505497356040393690402758557636039683075007984614264314802550433942617885990971202110511768121760826488944622697964930982921462840320850014092598270493079542993367042001339267321218767132063176291998391714014192946596879176425904447127657664796094937171819714510504836456988487840790317576922986001688147359646287894578550322731904860694734616037751755921771706899493873123836562784063321
    m = bytes_to_long(flag)
    c = pow(m, e, n) 
    

Solution

On each connection, we are given a flag encrypted using RSA, with additional information in the form

\[(p - a)^2 + (q - b)^2 = w\]

On every connection, the integers $a,b,w$ are different, although $a,b$ are usually small ($a,b < 2000$ ).

Lyutoon and Ratman noticed that factoring $z$, it was always a seventh power $w = z^t$, which means we can write the equation as:

\[x^2 + y^2 = z^7\]

We can factor the left hand side by writing:

\[x^2 + y^2 = (x + iy)(x - iy)\]

and now we realise that by factoring $z^7$ as a Gaussian integer in $\mathbb{Z}[i]$:

\[z = \prod_i (a_i + i b_i)\]

we can obtain $x,y$, as $(x + i y)$ will be a divisor of $z \in \mathbb{Z}[i]$, and from this solve for $p,q$ to grab the flag.

Connecting again, we get:

a = 2265 
b = 902 
w = 24007015341450638047707811509679207068051724063799752621201994109462561550079479155110637624506028551099549192036601169213196430196182069103932872524092047760624845002308713558682251660517182097667675473038586407097498167776645896369165963981698265040400341878755056463554861788991872633206414266159558715922583613630387512303492920597052611976890648632123534922756985895479931541478630417251021677032459939450624439421018438357005854556082128718286537575550378203702362524442461229
flag_enc = 10564879569008106132040759805988959471544940722100428235462653367215001622634768902220485764070394703676633460036566842009467954832811287152142597331508344786167188766356935684044757086902094847810694941751879500776345600036096556068243767090470376672110936445246103465175956767665996275085293250901512809704594905257754009538501795362031873203086994610168776981264025121998840163864902563628991590207637487738286741829585819040077197755226202284847

Obtaining the factors of $z \in \mathbb{Z}[i]$ we find:

a = 2265 
b = 902 
z = w^(1/7)
K = ZZ[i]
gaussian_factors = factor(K(z))
# gaussian_factors (-I) * (-1236649975237776943493190425869173*I - 3575914522629734831030006136433790) * (-5*I - 4) * (4*I + 5) * (-1236649975237776943493190425869173*I + 3575914522629734831030006136433790)

We now know that $(x + iy)$ is some divisor of $z$, and knowing that $p,q$ are prime, we can find these easily

z_test = (-1236649975237776943493190425869173*I - 3575914522629734831030006136433790)*(4*I + 5)
w_test = z_test**7
x_test = abs(w_test.imag())
y_test = abs(w_test.imag())
p = x_test + a
q = y_test + b

assert is_prime(p)
assert is_prime(q)
assert (p - a)**2 + (q - b)**2 == w

Finally, with p,q we can solve for the flag

from Crypto.Util.number import *

p = 3515251100858858796435724523870761115321577101490666287216209907489403476079222276536571942496157069855565014771125798502774268554017196492328530962886884456876064742139864478104832820555776577341055529681241338289453827370647829795170813667  
q = 3413213301181339793171422358348736699126965473930685311400429872075816456893055375667482794611435574843396575239764759040242158681190020317082329009191911152126267671754529169503180596722173728126136891139303943035843711591741985591269095977
phi = (p-1)*(q-1)
d = pow(0x10001, -1, phi)
print(long_to_bytes(pow(flag_enc,d,p*q)))
b'CCTF{Congrats_Y0u_5OLv3d_x**2+y**2=z**7}'

Flag

CCTF{Congrats_Y0u_5OLv3d_x**2+y**2=z**7}

RSAphantine

Challenge

RSA and solving equations, but should be a real mathematician to solve it with a diophantine equation?

2*z**5 - x**3 + y*z = 47769864706750161581152919266942014884728504309791272300873440765010405681123224050402253883248571746202060439521835359010439155922618613520747411963822349374260144229698759495359592287331083229572369186844312169397998958687629858407857496154424105344376591742814310010312178029414792153520127354594349356721
x**4 + y**5 + x*y*z = 89701863794494741579279495149280970802005356650985500935516314994149482802770873012891936617235883383779949043375656934782512958529863426837860653654512392603575042842591799236152988759047643602681210429449595866940656449163014827637584123867198437888098961323599436457342203222948370386342070941174587735051
y**6 + 2*z**5 + z*y = 47769864706750161581152919266942014884728504309791272300873440765010405681123224050402253883248571746202060439521835359010439155922618613609786612391835856376321085593999733543104760294208916442207908167085574197779179315081994735796390000652436258333943257231020011932605906567086908226693333446521506911058
p = nextPrime(x**2 + z**2 + y**2 << 76)
q = nextPrime(z**2 + y**3 - y*x*z ^ 67)
n, e = p * q, 31337
m = bytes_to_long(FLAG)
c = pow(m, e, n)
c = 486675922771716096231737399040548486325658137529857293201278143425470143429646265649376948017991651364539656238516890519597468182912015548139675971112490154510727743335620826075143903361868438931223801236515950567326769413127995861265368340866053590373839051019268657129382281794222269715218496547178894867320406378387056032984394810093686367691759705672

Solution

This challenge gives us the following set of three equations and three unknowns $x$, $y$, and $z$; it then generates parameters for RSA encryption using the following equations:

\[p = \text{nextPrime}(\frac{x^2+y^2+z^2}{2^{76}})\\ q = \text{nextPrime}(z^2+y^3- (xyz \oplus 67))\]

It doesn’t look like we can attack the equations for $p$ or $q$ directly, so we solve the diophantine equations first:

\[2z^5-x^3+yz=47769... = a\\ x^4+y^5+xyz=89701... = b\\ y^6+2z^5+yz=47769... = c\]

Note that while the right hand side of the first and third equations appear to be the same, they are different numbers. We first compute $c-a = x^3+y^6 = (x+y^2)(x^2-xy^2+y^4)$ by sum of cubes; factoring $c-a$, we recover the factors $3133713317731333$ and $28413320364759425…$.

Plugging the equations into z3, we solve for $x$, $y$, and $z$:

from z3 import *
from sympy import *

A = 3133713317731333
B = 28413320364759425177418147555143516002041291710972733253944530195017276664069717887927099709630886727522090965378073004342203980057853092114878433424202989
c = 486675922771716096231737399040548486325658137529857293201278143425470143429646265649376948017991651364539656238516890519597468182912015548139675971112490154510727743335620826075143903361868438931223801236515950567326769413127995861265368340866053590373839051019268657129382281794222269715218496547178894867320406378387056032984394810093686367691759705672

x = Int("x")
y = Int("y")
z = Int("z")

s = Solver()

s.add(y**2 + x == A)
s.add(y**4 - x*y**2 + x**2 == B)
s.add(y>0)
s.add(2*z**5 - x**3 + y*z == 47769864706750161581152919266942014884728504309791272300873440765010405681123224050402253883248571746202060439521835359010439155922618613520747411963822349374260144229698759495359592287331083229572369186844312169397998958687629858407857496154424105344376591742814310010312178029414792153520127354594349356721)
s.add(x**4 + y**5 + x*y*z == 89701863794494741579279495149280970802005356650985500935516314994149482802770873012891936617235883383779949043375656934782512958529863426837860653654512392603575042842591799236152988759047643602681210429449595866940656449163014827637584123867198437888098961323599436457342203222948370386342070941174587735051)
s.add(y**6 + 2*z**5 + z*y == 47769864706750161581152919266942014884728504309791272300873440765010405681123224050402253883248571746202060439521835359010439155922618613609786612391835856376321085593999733543104760294208916442207908167085574197779179315081994735796390000652436258333943257231020011932605906567086908226693333446521506911058)

if s.check() == sat:
    m = s.model()
    x = m[x].as_long()
    y = m[y].as_long()
    z = m[z].as_long()
    p = nextprime(x**2 + z**2 + y**2 << 76)
    q = nextprime(z**2 + y**3 - y*x*z ^ 67)
    d = pow(31337, -1, (p-1)*(q-1))
    print(bytes.fromhex(hex(pow(c, d, p*q))[2:]).decode())

Flag

CCTF{y0Ur_jO8_C4l13D_Diophantine_An4LySI5!}

Frozen

Challenge

The server implements a signature scheme where we can get the parameters, the public key, and a signature for one sample message. We have to forge the signature for a second message.

The key generation works as follows:

Start with a prime $p$ and random $r$, which we know. We work in $\mathbb{Z}_p$, so everything below is implicitly done modulo $p$.
Pick a random $r$, which we don’t know.
Build the array $U_i = r^{i+1}s$.
For the public key $pub$, take $U$ and mask the bottom 32 bits of each element.
The remaining bottom 32 bits of each element are the private key $priv$.

To sign a message $M_i$, interpreted as an array of 32-bit integers:

Let $q$ be a prime larger than all elements of $M$.
The signature is $sig_i = M_i priv_i \text{ mod } q$.

#!/usr/bin/env python3

from Crypto.Util.number import *
from gmpy2 import *
import sys, random, string

flag = 'fakeflag{}'

def genrandstr(N):
    return ''.join(random.choice(string.ascii_uppercase + string.digits + string.ascii_lowercase) for _ in range(N))

def paramaker(nbit):
    p = getPrime(nbit)
    r = getRandomRange(1, p)
    return p, r

def keygen(params, l, d):
    p, r = params
    s = getRandomRange(1, p)
    U = [pow(r, c + 1, p) * s % p for c in range(0,l)]
    V = [int(bin(u)[2:][:-d] + '0' * d, 2) for u in U]
    S = [int(bin(u)[2:][-d:], 2) for u in U]
    privkey, pubkey = S, V
    return pubkey, privkey

def sign(msg, privkey, d):
    msg = msg.encode('utf-8')
    l = len(msg) // 4
    M = [bytes_to_long(msg[4*i:4*(i+1)]) for i in range(l)]
    q = int(next_prime(max(M)))
    sign = [M[i]*privkey[i] % q for i in range(l)]
    return sign

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, " hi young cryptographers, welcome to the frozen signature battle!!  ", border)
    pr(border, " Your mission is to forge the signature for a given message, ready?!", border)
    pr(border*72)

    randstr = genrandstr(20)
    nbit, dbit = 128, 32
    params = paramaker(nbit)
    l = 5
    pubkey, privkey = keygen(params, l, dbit)

    while True:
        pr("| Options: \n|\t[S]how the params \n|\t[P]rint pubkey \n|\t[E]xample signature \n|\t[F]orge the signature \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 's':
            pr(f'| p = {params[0]}')
            pr(f'| r = {params[1]}')
        elif ans == 'p':
            pr(f'pubkey = {pubkey}')
        elif ans == 'e':
            pr(f'| the signature for "{randstr}" is :')
            pr(f'| signature = {sign(randstr, privkey, dbit)}')
        elif ans == 'f':
            randmsg = genrandstr(20)
            pr(f'| send the signature of the following message like example: {randmsg}')
            SIGN = sc()
            try:
                SIGN = [int(s) for s in SIGN.split(',')]
            except:
                die('| your signature is not valid! Bye!!')
            if SIGN == sign(randmsg, privkey, dbit):
                die(f'| Congrats, you got the flag: {FLAG}')
            else:
                die(f'| Your signature is not correct, try later! Bye!')
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

Solution

If we look at the first element of the signature, we have:

\[sig_0 = M_0 priv_0 \text{ mod } q\]

Since we can compute $q$ (as we know the message $M$), we can find the multiplicative inverse of $M_0$ and recover the first element of the private key modulo $q$:

\[priv_0 = M_0^{-1} sig_0 \text{ mod } q\]

The real private key is 32 bits long, and $q$ is around $2^{30}$, so around one try in four this will be the real value of $priv_0$. If this doesn’t work, we can proceed by trying $M^0{-1} sig_0 + kq$ for increasing values of $k$, and will recover the correct $priv_0$ in a few tries.

For each candidate value, we can combine it with $pub_0$ to get $U_0 = rs$. Since we know $r$, we have $s = U_0 r^{-1}$ (in $\mathbb{Z}_p$), which we can use to re-generate the entire public and private key and see if the public key matches the one we were given.

Once we find one that does, all that’s left is to use the provided signing function to forge the signature.

Here is a hacky script written during the CTF – it doesn’t work properly when the recovered $priv_0$ is wrapped by the modulus, but that just means we need to run it a few times to get the flag:

#! /usr/bin/env python
from pwn import *
from Crypto.Util.number import *
from gmpy2 import *

l = 5

def keygen(params, l, d, s):
    p, r = params
    U = [pow(r, c + 1, p) * s % p for c in range(0,l)]

    V = [int(bin(u)[2:][:-d] + '0' * d, 2) for u in U]
    S = [int(bin(u)[2:][-d:], 2) for u in U]
    privkey, pubkey = S, V

    return pubkey, privkey


def sign(msg, privkey, d):
    msg = msg.encode('utf-8')
    l = len(msg) // 4
    M = [bytes_to_long(msg[4*i:4*(i+1)]) for i in range(l)]
    q = int(next_prime(max(M)))
    sign = [M[i]*privkey[i] % q for i in range(l)]
    return sign

    
def break_key(p, r, pubkey, msg, sig):
    q = int(next_prime(max(msg)))
    pk0_base = (sig[0] * pow(msg[0], -1, q)) % q
    print(pk0_base, sig[0], pow(msg[0], -1, q))

    for pk0 in range(pk0_base, q, 2**32):
        rs = pubkey[0] + pk0
        s = (rs * pow(r, -1, p)) % p

        outpub, outpriv = keygen((p, r), 5, 32, s)
        print(pubkey, outpub)
        if outpub == pubkey:
            return outpub, outpriv

    raise Exception("Could not find key!")


serv = pwnlib.tubes.remote.remote('03.cr.yp.toc.tf', 25010)
#serv = pwnlib.tubes.process.process('./frozen.py')

serv.recvuntil('[Q]uit')
serv.sendline('s')
serv.readline()

p = int(serv.readline().rstrip().split()[-1])
r = int(serv.readline().rstrip().split()[-1])
print('p =', p)
print('r =', r)

serv.recvuntil('[Q]uit')

serv.sendline('e')
serv.readline()
msg_b = serv.recvline().decode('utf-8').split('"')[1]
sig = eval(serv.recvline().decode('utf-8').split('=')[1])  # lol
msg = [bytes_to_long(msg_b.encode('utf-8')[4*i:4*(i+1)]) for i in range(l)]

print('msg =', msg)
print('sig =', sig)

serv.recvuntil('[Q]uit')
serv.sendline('p')
serv.readline()
pubkey = eval(serv.recvline().decode('utf-8').split('=')[1])  # lol again

print('pubkey =', pubkey)

pub, priv = break_key(p, r, pubkey, msg, sig)

serv.recvuntil('[Q]uit')
serv.sendline('f')
serv.readline()
forge = serv.recvline().rstrip().decode('utf-8').split()[-1]

forge_sig = sign(forge, priv, 32)

serv.sendline(','.join(str(x) for x in forge_sig))
serv.interactive()

Flag

CCTF{Lattice_bA5eD_T3cHn1QuE_70_Br34K_LCG!!}

LINDA

Challenge

Dan Boneh loves to improve cryptosystems, you should be loving breaking them? nc 07.cr.yp.toc.tf 31010

linda.txz

#!/usr/bin/env python3

from Crypto.Util.number import *
from math import gcd
from flag import flag

def keygen(p):
    while True:
        u = getRandomRange(1, p)
        if pow(u, (p-1) // 2, p) != 1:
            break
    x = getRandomRange(1, p)
    w = pow(u, x, p)
    while True:
        r = getRandomRange(1, p-1)
        if gcd(r, p-1) == 1:
            y = x * inverse(r, p-1) % (p-1)
            v = pow(u, r, p)
            return u, v, w
    
def encrypt(m, pubkey):
    p, u, v, w = pubkey
    assert m < p
    r, s = [getRandomRange(1, p) for _ in '01']
    ca = pow(u, r, p)
    cb = pow(v, s, p)
    cc = m * pow(w, r + s, p) % p
    enc = (ca, cb, cc)
    return enc

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, "  .:::::: LINDA Cryptosystem has high grade security level ::::::.  ", border)
    pr(border, "  Can you break this cryptosystem and find the flag?                ", border)
    pr(border*72)

    pr('| please wait, preparing the LINDA is time consuming...')
    from secret import p
    u, v, w = keygen(p)
    msg = bytes_to_long(flag)
    pubkey = p, u, v, w
    enc = encrypt(msg, pubkey)
    while True:
        pr("| Options: \n|\t[E]xpose the parameters \n|\t[T]est the encryption \n|\t[S]how the encrypted flag \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 'e':
            pr(f'| p = {p}')
            pr(f'| u = {u}')
            pr(f'| v = {v}')
            pr(f'| w = {w}')
        elif ans == 's':
            print(f'enc = {enc}')
        elif ans == 't':
            pr('| send your message to encrypt: ')
            m = sc()
            m = bytes_to_long(m.encode('utf-8'))
            pr(f'| encrypt(m) = {encrypt(m, pubkey)}')
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

Solution

By interacting with the challenge, we can get public key parameters by sending e, get encrypted flag with s, encrypt our own messages with t and quit with q. Only the first two options will be relevant to the solution.

Encryption here works like this: $p, u, v, w$ are public key parameters, message $m$ is encrypted as follows:

\[ca \equiv u^r \mod p \\ cb \equiv v^s \mod p$ \\ cc \equiv mw^{r + s} \mod p\]

where $r, s$ are uniformly random numbers from $[1;p]$.

We can notice that despite $p$ being new on each connection, $p - 1$ is always smooth. Example:

p = 31236959722193405152010489304408176327538432524312583937104819646529142201202386217645408893898924349364771709996106640982219903602836751314429782819699
p - 1 = 2 * 3 * 11 * 41 * 137 * 223 * 7529 * 14827 * 15121 * 40559 * 62011 * 429083 * 916169 * 3810461 * 4316867 * 20962993 * 31469027 * 81724477 * 132735437 * 268901797 * 449598857 * 2101394579 * 2379719473 * 5859408629 * 11862763021 * 45767566217

This is the key for solving this challenge, because after getting public key paramters and encrypted flag we can factor $p - 1$ by using trial division and ECM, then use Pohlig-Hellman algorithm to compute $r, s$ as discrete logarithms of $ca, cb$ with bases $u, v$ respectively even without trying to find weaknesses in the keygen process. Then we can compute $m \equiv ccw^{-(r + s)} \mod p$ and get the flag.

#!/usr/bin/env sage
from minipwn import remote # mini-pwntools library to connect to server
from Crypto.Util.number import long_to_bytes

rem = remote("07.cr.yp.toc.tf", 31010)
for _ in range(10):
    rem.recvline()
rem.sendline('e')
p = int(rem.recvline()[6:])
u = int(rem.recvline()[6:])
v = int(rem.recvline()[6:])
w = int(rem.recvline()[6:])
for _ in range(5):
    rem.recvline()
rem.sendline('s')
ca, cb, cc = map(int, rem.recvline()[7:-2].split(b', '))
r = discrete_log(Mod(ca, p), Mod(u, p)) # sage has built-in discrete logarithm function, which uses Pohlig-Hellman
s = discrete_log(Mod(cb, p), Mod(v, p)) # algorithm and automatically determines and factors group order, which divides p - 1
m = cc * power_mod(w, -(r + s), p) % p
print(long_to_bytes(m).decode())

Flag

CCTF{1mPr0v3D_CrYp7O_5yST3m_8Y_Boneh_Boyen_Shacham!}