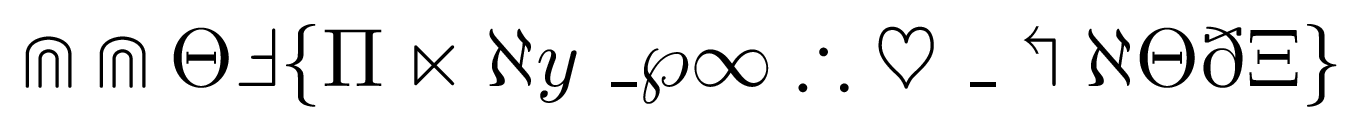CryptoCTF 2021 - Easy
Last week, CryptoHackers got together to play CryptoCTF for the second time as a team. We solved 26/29 of the challenges during the 24 hour window and came third overall. First and second places went to Super Guessers (Rkm and Rbtree are very friendly faces from CryptoHack) and a Vietnamese team working together to support the spirit of Ho Chi Minh city and nearby provinces. Congratulations to them both.
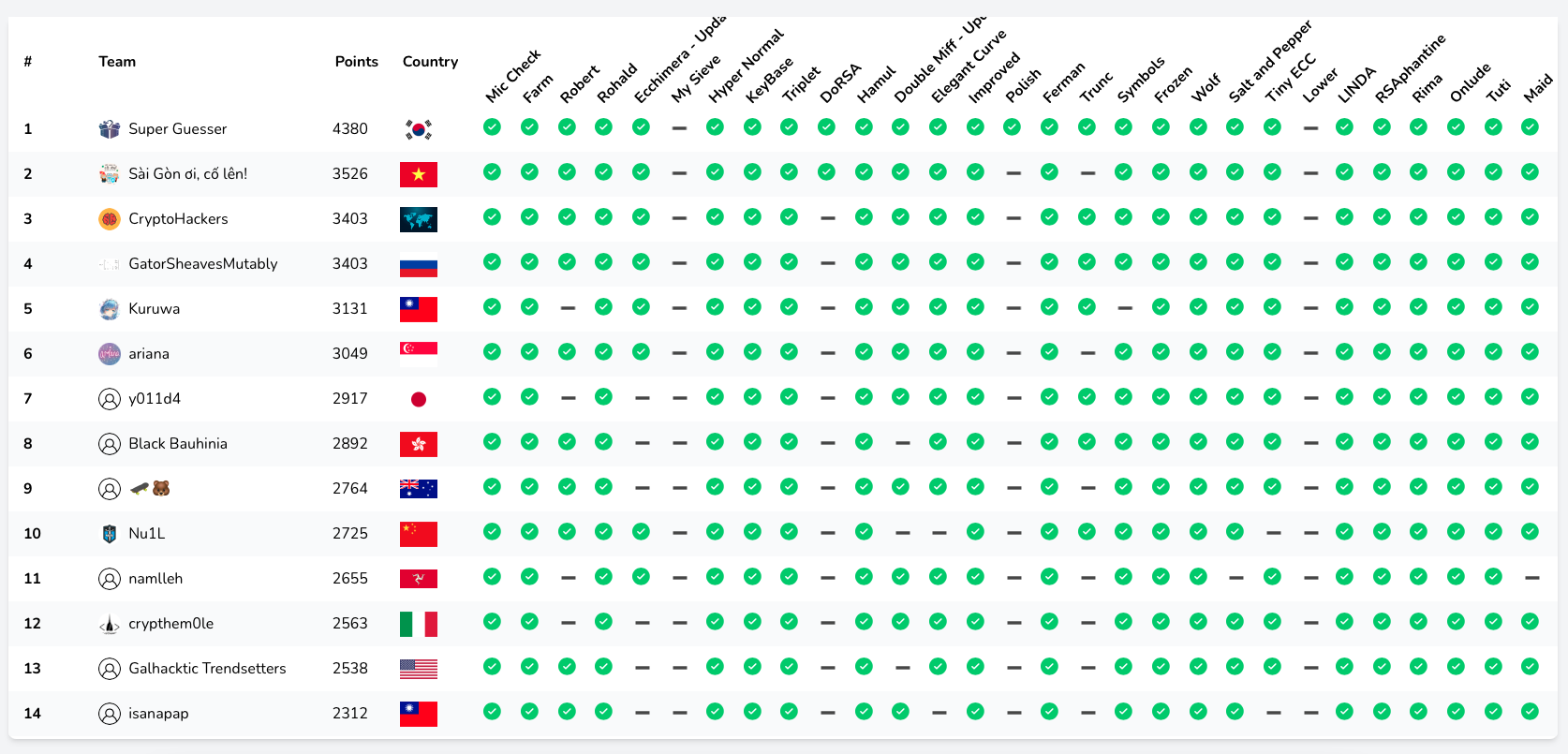
Not only was it a lot of fun for us all to play together, but it was amazing to see how many CryptoHack friends played the CTF either solo or in small teams and who were able to get a top 15 spot. We’re honoured to have so many talented people in our Discord, chatting with us about maths and cryptography. We even have guest writeups from rkm0959 talking about the solutions of DoRSA and Polish.
Here are the write-ups for the easiest challenges in the CTF. You can find write ups for the medium and hard challenges as other posts on our blog.
Thank you to everyone who played for the CryptoHackers, and to ASIS CTF for organising this enjoyable event. Congratulations again to Super Guessers for being the ultimate crypto heros!
We will be publishing more writeups here as soon as they are finished. If you spot a mistake or an improvement that could be made, please ping jack or hyperreality on CryptoHack Discord.
Challenges
| Challenge Name | Category | Solved By | Points |
|---|---|---|---|
| Farm | Finite Fields | evilmuffinha | 41 |
| Keybase | AES | UnblvR (Coming Soon) | 48 |
| Rima | Encoding | Willwam845, randomdude999 | 56 |
| Symbols | Misc | Q7 | 70 |
| Hyper Normal | Misc | Q7 | 71 |
| Salt and Pepper | Hash length extension | Willwam845 | 71 |
| Titu | Diophantine equations | Jack | 69 |
| Hamul | RSA | Lyutoon | 83 |
Farm
Challenge
Explore the Farm very carefully!
#!/usr/bin/env sage
from sage.all import *
import string, base64, math
from flag import flag
ALPHABET = string.printable[:62] + '\\='
F = list(GF(64))
def keygen(l):
key = [F[randint(1, 63)] for _ in range(l)]
key = math.prod(key) # Optimization the key length :D
return key
def maptofarm(c):
assert c in ALPHABET
return F[ALPHABET.index(c)]
def encrypt(msg, key):
m64 = base64.b64encode(msg)
enc, pkey = '', key**5 + key**3 + key**2 + 1
for m in m64:
enc += ALPHABET[F.index(pkey * maptofarm(chr(m)))]
return enc
# KEEP IT SECRET
key = keygen(14) # I think 64**14 > 2**64 is not brute-forcible :P
enc = encrypt(flag, key)
print(f'enc = {enc}')
The key is the product of 14 random elements selected from $GF(64)$.
Solution
Note that the product of two elements of $GF(64)$ is still an element of $GF(64)$. Inductively, the key lies in $GF(64)$. That is, the key space is just 64 and hence we are able to brute-force the key.
Implementation
#!/usr/bin/env sage
import string
import base64
enc = "805c9GMYuD5RefTmabUNfS9N9YrkwbAbdZE0df91uCEytcoy9FDSbZ8Ay8jj"
ALPHABET = string.printable[:62] + '\\='
F = list(GF(64))
def farmtomap(f):
assert f in F
return ALPHABET[F.index(f)]
def decrypt(msg, key):
dec, pkey = '', key**5 + key**3 + key**2 + 1
for m in msg:
dec += farmtomap(F[ALPHABET.index(m)] / pkey)
return base64.b64decode(dec)
for possible_key in F:
try:
plaintext = decrypt(enc, possible_key)
if b"CCTF{" in plaintext:
print(plaintext.decode())
except:
continue
Flag
CCTF{EnCrYp7I0n_4nD_5u8STitUtIn9_iN_Fi3Ld!}
Keybase
Challenge
Recovering secrets is hard, but there is always some easy parts!
nc 01.cr.yp.toc.tf 17010
#!/usr/bin/env python3
from Crypto.Util import number
from Crypto.Cipher import AES
import os, sys, random
from flag import flag
def keygen():
iv, key = [os.urandom(16) for _ in '01']
return iv, key
def encrypt(msg, iv, key):
aes = AES.new(key, AES.MODE_CBC, iv)
return aes.encrypt(msg)
def decrypt(enc, iv, key):
aes = AES.new(key, AES.MODE_CBC, iv)
return aes.decrypt(enc)
def die(*args):
pr(*args)
quit()
def pr(*args):
s = " ".join(map(str, args))
sys.stdout.write(s + "\n")
sys.stdout.flush()
def sc():
return sys.stdin.readline().strip()
def main():
border = "+"
pr(border*72)
pr(border, " hi all, welcome to the simple KEYBASE cryptography task, try to ", border)
pr(border, " decrypt the encrypted message and get the flag as a nice prize! ", border)
pr(border*72)
iv, key = keygen()
flag_enc = encrypt(flag, iv, key).hex()
while True:
pr("| Options: \n|\t[G]et the encrypted flag \n|\t[T]est the encryption \n|\t[Q]uit")
ans = sc().lower()
if ans == 'g':
pr("| encrypt(flag) =", flag_enc)
elif ans == 't':
pr("| Please send your 32 bytes message to encrypt: ")
msg_inp = sc()
if len(msg_inp) == 32:
enc = encrypt(msg_inp, iv, key).hex()
r = random.randint(0, 4)
s = 4 - r
mask_key = key[:-2].hex() + '*' * 4
mask_enc = enc[:r] + '*' * 28 + enc[32-s:]
pr("| enc =", mask_enc)
pr("| key =", mask_key)
else:
die("| SEND 32 BYTES MESSAGE :X")
elif ans == 'q':
die("Quitting ...")
else:
die("Bye ...")
if __name__ == '__main__':
main()
Solution
from pwn import *
from Crypto.Cipher import AES
def bxor(s1,s2):
return b''.join(bytes([a ^ b]) for a,b in zip(s1,s2))
r = remote("01.cr.yp.toc.tf", 17010)
# [G]et the encrypted flag
r.sendlineafter("[Q]uit\n", "G")
enc_flag = bytes.fromhex(r.recvline().strip().decode().split(" = ")[1])
# [T]est the encryption
# Loop this a few times until we get 4 characters of the plaintext in the beginning
# as this makes the brute-force a bit easier code-wise
while True:
r.sendlineafter("[Q]uit\n", "T")
r.sendlineafter("Please send your 32 bytes message to encrypt: \n", b"A"*32)
enc = r.recvline().strip().decode().split(" = ")[1]
key = r.recvline().strip().decode().split(" = ")[1]
prefix = enc.split("*")[0]
if len(prefix) == 4:
prefix = bytes.fromhex(prefix)
break
# Brute force the last 2 bytes of the key
key = bytearray.fromhex(key[:-4]) + b"\x00\x00"
for k1 in range(256):
key[-2] = k1
for k2 in range(256):
key[-1] = k2
# Decrypt the second block alone, without CBC/IV, and XOR with the two unmasked bytes.
# Result should be original plaintext "AA.....".
if bxor(AES.new(key, AES.MODE_ECB).decrypt(bytes.fromhex(enc[-32:])), b"AA") == prefix:
# Recover full first block by xoring second block with known plaintext
block = bxor(AES.new(key, AES.MODE_ECB).decrypt(bytes.fromhex(enc[-32:])), b"A"*16)
# IV is whatever the first block was XORed with prior to encryption. Decrypt and XOR.
IV = bxor(AES.new(key, AES.MODE_ECB).decrypt(block), b"A"*16)
print(f"Recovered key candidate: {key.hex()} with IV {IV.hex()}")
print(AES.new(key, AES.MODE_CBC, IV).decrypt(enc_flag))
Flag
CCTF{h0W_R3cOVER_7He_5eCrET_1V?}
Rima
Challenge
#!/usr/bin/env python3
from Crypto.Util.number import *
from flag import FLAG
def nextPrime(n):
while True:
n += (n % 2) + 1
if isPrime(n):
return n
f = [int(x) for x in bin(int(FLAG.hex(), 16))[2:]]
f.insert(0, 0)
for i in range(len(f)-1): f[i] += f[i+1]
a = nextPrime(len(f))
b = nextPrime(a)
g, h = [[_ for i in range(x) for _ in f] for x in [a, b]]
c = nextPrime(len(f) >> 2)
for _ in [g, h]:
for __ in range(c): _.insert(0, 0)
for i in range(len(_) - c): _[i] += _[i+c]
g, h = [int(''.join([str(_) for _ in __]), 5) for __ in [g, h]]
for _ in [g, h]:
if _ == g:
fname = 'g'
else:
fname = 'h'
of = open(f'{fname}.enc', 'wb')
of.write(long_to_bytes(_))
of.close()
The flag is encoded using a bunch of weird looking operations, and then we get the two files g.enc and h.enc
Solution
Firstly, we can deduce the flag length as 32 bytes by simply testing some letter repeated some number of times as the flag, then checking the length of the output and comparing it to the size of g.enc.
We will work through the steps in reverse order.
Step 1
g, h = [int(''.join([str(_) for _ in __]), 5) for __ in [g, h]]
for _ in [g, h]:
if _ == g:
fname = 'g'
else:
fname = 'h'
of = open(f'{fname}.enc', 'wb')
of.write(long_to_bytes(_))
of.close()
Firstly, each file contains bytes, which we need to convert to a base 10 integer. Then, we need to convert this base 10 integer into a base 5 integer. We can do this quite easily with gmpy2’s digits function.
Step 2
c = nextPrime(len(f) >> 2)
for _ in [g, h]:
for __ in range(c): _.insert(0, 0)
for i in range(len(_) - c): _[i] += _[i+c]
These next steps add some elements of the list to other elements of the list. We can work out the value of len(_) - c by just running the program with a random 32 byte flag, and then to reverse it, we just need to ensure that we change the addition to subtraction, and work in reverse order, as the later elements of the list are not affected by the earlier ones (but not vice versa).
We also then need to trim $c$ amound of 0’s from the start of the list at the end. $c$ can again be worked out by just running the program.
Step 3
a = nextPrime(len(f))
b = nextPrime(a)
g, h = [[_ for i in range(x) for _ in f] for x in [a, b]]
This step simply takes the list $f$ and duplicates it $a$ and $b$ times, storing them in $g$ and $h$. We can either manually find the repeating sequence, work out the values of $a$ and $b$ and simply split $g$ into $a$ chunks (or $h$ into $b$ chunks), or we can simply know the length of $f$, and take the first $len(f)$ elements of $g$ to get the original $f$.
Step 4
f = [int(x) for x in bin(int(FLAG.hex(), 16))[2:]]
f.insert(0, 0)
for i in range(len(f)-1): f[i] += f[i+1]
Our last step is again quite similar to step 2, we work out the length of $f$ by running the program, and then going in reverse order, changing the addition to a subtraction instead. We can then obtain the flag by converting the list into a string, which should be the binary string of the flag.
Implementation
Putting this all together, this looks like this:
from gmpy2 import digits
# Step 1
g = list(digits(bytes_to_long(open("g.enc","rb").read()) ,5))
g = [int(x) for x in g]
# Step 2
for _ in [g]:
for i in range(65791,-1,-1): _[i] -= _[i+c]
# Step 3
f = g[67:67+256]
f = [int(x) for x in f]
# Step 4
for i in range(len(f)-2, -1, -1):f[i] -= f[i+1]
print("".join([str(x) for x in f]))
Flag
CCTF{_how_finD_7h1s_1z_s3cr3T?!}
Symbols
Challenge
Oh, my eyes, my eyes! People still can solve this kind of cryptography? Mathematicians should love this one!
Solution
In this challenge, we are given an image of math symbols, from the first couple of symbols and the flag format, we can guess that the flag is the initials of these symbols in $\LaTeX$.
By using Mathpix Snip, a tool that can convert images into LaTeX for inline equations, we can get most of the symbols and get the flag.
\[\Cap \Cap \Theta \Finv \{ \Pi \ltimes \aleph y \_ \wp \infty \therefore \heartsuit \_ \Lsh \aleph \Theta \eth \Xi \}\]\Cap \Cap \Theta \Finv \{ \Pi \ltimes \aleph y \_ \wp \infty \therefore \heartsuit \_ \Lsh \aleph \Theta \eth \Xi \}
Flag
CCTF{Play_with_LaTeX}
Hyper Normal
Challenge
Being normal is hard these days because of Corona virus pandemic!
#!/usr/bin/env python3
import random
from flag import FLAG
p = 8443
def transpose(x):
result = [[x[j][i] for j in range(len(x))] for i in range(len(x[0]))]
return result
def vsum(u, v):
assert len(u) == len(v)
l, w = len(u), []
for i in range(l):
w += [(u[i] + v[i]) % p]
return w
def sprod(a, u):
w = []
for i in range(len(u)):
w += [a*u[i] % p]
return w
def encrypt(msg):
l = len(msg)
hyper = [ord(m)*(i+1) for (m, i) in zip(list(msg), range(l))]
V, W = [], []
for i in range(l):
v = [0]*i + [hyper[i]] + [0]*(l - i - 1)
V.append(v)
random.shuffle(V)
for _ in range(l):
R, v = [random.randint(0, 126) for _ in range(l)], [0]*l
for j in range(l):
v = vsum(v, sprod(R[j], V[j]))
W.append(v)
random.shuffle(transpose(W))
return W
enc = encrypt(FLAG)
print(enc)
Solution
This challenge gives a strange encryption scheme. This encryption algorithm actually does this. For an input of length $l$, the algorithm first multiplies each character of the input by the corresponding index to obtain a vector $x$. Then the algorithm loops $l$ times, each time outputs a vector $v$. Each number in the vector $v$ is a random number between 0 and 126 multiplied by the corresponding number in the vector $x$. All these operations are performed modulo 8443.
It is worth noting that random.shuffle on line 38 of the program actually has no effect on the output, because the transpose function returns a new object.
Solving for the input is intuitive. For the i-th byte of the input, we simply iterate through all printable characters, multiply $i$ by those characters, and multiply 0 through 126 to get all possible results. If column $i$ of the program output happens to be a subset of the possible results generated by a character $c$, then the i-th byte of the input is likely to be $c$.
#!/usr/bin/env python3
from string import printable
p = 8443
with open('output.txt', 'r') as f:
enc = eval(f.read())
results = []
for i in range(len(enc[0])):
tmp = []
for j in enc:
tmp.append(j[i])
results.append(tmp)
flag = ''
for idx, result in enumerate(results):
for c in printable:
possibilities = [ord(c)*i*(idx+1) % p for i in range(127)]
if all([i in possibilities for i in result]):
flag += c
break
print(flag)
Flag
CCTF{H0w_f1Nd_th3_4lL_3I9EnV4Lu35_iN_FiN173_Fi3lD5!???}
Salt and Pepper
Challenge
#!/usr/bin/env python3
from hashlib import md5, sha1
import sys
from secret import salt, pepper
from flag import flag
assert len(salt) == len(pepper) == 19
assert md5(salt).hexdigest() == '5f72c4360a2287bc269e0ccba6fc24ba'
assert sha1(pepper).hexdigest() == '3e0d000a4b0bd712999d730bc331f400221008e0'
def auth_check(salt, pepper, username, password, h):
return sha1(pepper + password + md5(salt + username).hexdigest().encode('utf-8')).hexdigest() == h
def die(*args):
pr(*args)
quit()
def pr(*args):
s = " ".join(map(str, args))
sys.stdout.write(s + "\n")
sys.stdout.flush()
def sc():
return sys.stdin.readline().strip()
def main():
border = "+"
pr(border*72)
pr(border, " welcome to hash killers battle, your mission is to login into the ", border)
pr(border, " ultra secure authentication server with provided information!! ", border)
pr(border*72)
USERNAME = b'n3T4Dm1n'
PASSWORD = b'P4s5W0rd'
while True:
pr("| Options: \n|\t[L]ogin to server \n|\t[Q]uit")
ans = sc().lower()
if ans == 'l':
pr('| send your username, password as hex string separated with comma: ')
inp = sc()
try:
inp_username, inp_password = [bytes.fromhex(s) for s in inp.split(',')]
except:
die('| your input is not valid, bye!!')
pr('| send your authentication hash: ')
inp_hash = sc()
if USERNAME in inp_username and PASSWORD in inp_password:
if auth_check(salt, pepper, inp_username, inp_password, inp_hash):
die(f'| Congrats, you are master in hash killing, and it is the flag: {flag}')
else:
die('| your credential is not valid, Bye!!!')
else:
die('| Kidding me?! Bye!!!')
elif ans == 'q':
die("Quitting ...")
else:
die("Bye ...")
if __name__ == '__main__':
main()
We send a username and password to the server, along with an authentication hash. These are all passed as parameters to the auth_check function, and the username containsn3T4Dm1n, the password contains P4s5W0rd, and the function returns true, we get the flag.
Solution
The check_auth function uses two secrets, salt and pepper, which we know the length of, however we don’t know the value of.
The check_auth function calculates the authentication hash using the following line
sha1(pepper + password + md5(salt + username).hexdigest().encode('utf-8')).hexdigest()
Since these two secrets are hashed as well as our username and password, we cannot directly work out the authentication hash. However, we get given the MD5 hash of salt, and the SHA1 hash of pepper. Since both of the secret values are put as prefixes to our input, we can perform a hash length extension attack.
HashPump is a useful tool to do this, as all we need to do is provide the parameters and the tool does most of the work for us. One thing that needed to be changed however is that since we get the raw hashes, we don’t have any data to give to the tool, and Hashpump complains when we do that.
To get around this, I simply removed this check in the main.cpp file (line 255) and recompiled it.
First, we will create a MD5 of (salt + padding + n3T4Dm1n) using the tool:
hashpump -s "5f72c4360a2287bc269e0ccba6fc24ba" -d "" -a "n3T4Dm1n" -k 19
giving an output of
95623660d3d04c7680a52679e35f041c
\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x98\x00\x00\x00\x00\x00\x00\x00n3T4Dm1n
Then, we will create our authentication hash by creating a SHA1 of (pepper + padding + P4s5W0rd + 95623660d3d04c7680a52679e35f041c)
hashpump -s "3e0d000a4b0bd712999d730bc331f400221008e0" -d "" -a "P4s5W0rd95623660d3d04c7680a52679e35f041c" -k 19
giving an output of
83875efbe020ced3e2c5ecc908edc98481eba47f
\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x98P4s5W0rd95623660d3d04c7680a52679e35f041c
83875efbe020ced3e2c5ecc908edc98481eba47f should now be our authentication hash when we use \x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x98\x00\x00\x00\x00\x00\x00\x00n3T4Dm1n as our username and \x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x98P4s5W0rd as our password (note that we remove the MD5 hash at the end as it gets added when the auth_check function is called).
Submitting these to the server gives us the flag.
Flag
CCTF{Hunters_Killed_82%_More_Wolves_Than_Quota_Allowed_in_Wisconsin}
Titu
Challenge
Cryptography is coupled with all kinds of equations very much!
#!/usr/bin/env python3
from Crypto.Util.number import *
from flag import flag
l = len(flag)
m_1, m_2 = flag[: l // 2], flag[l // 2:]
x, y = bytes_to_long(m_1), bytes_to_long(m_2)
k = '''
000bfdc32162934ad6a054b4b3db8578674e27a165113f8ed018cbe9112
4fbd63144ab6923d107eee2bc0712fcbdb50d96fdf04dd1ba1b69cb1efe
71af7ca08ddc7cc2d3dfb9080ae56861d952e8d5ec0ba0d3dfdf2d12764
'''.replace('\n', '')
assert((x**2 + 1)*(y**2 + 1) - 2*(x - y)*(x*y - 1) == 4*(int(k, 16) + x*y))
Given this source, the goal is to solve the equation to obtain both $x,y$.
Solution
Factoring $k$ we find that it is a perfect square
sage: factor(k)
2^2 * 3^2 * 11^4 * 19^2 * 47^2 * 71^2 * 3449^2 * 11953^2 * 5485619^2 * 2035395403834744453^2 * 17258104558019725087^2 * 1357459302115148222329561139218955500171643099^2
Which tells us that moving some terms around, we can write the left hand side as a perfect square too:
sage: f = (x**2 + 1)*(y**2 + 1) - 2*(x - y)*(x*y - 1) - 4*x*y
sage: f
x^2*y^2 - 2*x^2*y + 2*x*y^2 + x^2 - 4*x*y + y^2 + 2*x - 2*y + 1
sage: factor(f)
(y - 1)^2 * (x + 1)^2
So we can solve this challenge by looking at the divisors of $\sqrt{4k}$ as we have
\[(y - 1)^2 (x + 1)^2 = 4k = m\]This is easy using Sage’s divisors(m) function:
factors = [2, 2, 3, 11, 11, 19, 47, 71, 3449, 11953, 5485619, 2035395403834744453, 17258104558019725087, 1357459302115148222329561139218955500171643099]
m = prod(factors)
for d in divs:
x = long_to_bytes(d - 1)
if b'CCTF{' in x:
print(x)
y = (n // d) + 1
print(long_to_bytes(y))
b'CCTF{S1mPL3_4Nd_N!cE_D'
b'iophantine_EqUa7I0nS!}'
Flag
CCTF{S1mPL3_4Nd_N!cE_Diophantine_EqUa7I0nS!}
Hamul
Challenge
RSA could be hard, or easy?
#!/usr/bin/env python3
from Crypto.Util.number import *
from flag import flag
nbit = 64
while True:
p, q = getPrime(nbit), getPrime(nbit)
P = int(str(p) + str(q))
Q = int(str(q) + str(p))
PP = int(str(P) + str(Q))
QQ = int(str(Q) + str(P))
if isPrime(PP) and isPrime(QQ):
break
n = PP * QQ
m = bytes_to_long(flag.encode('utf-8'))
if m < n:
c = pow(m, 65537, n)
print('n =', n)
print('c =', c)
# n = 98027132963374134222724984677805364225505454302688777506193468362969111927940238887522916586024601699661401871147674624868439577416387122924526713690754043
# c = 42066148309824022259115963832631631482979698275547113127526245628391950322648581438233116362337008919903556068981108710136599590349195987128718867420453399
Solution
Since we can see that the generation of $PP$ and $QQ$ is special:
while True:
p, q = getPrime(nbit), getPrime(nbit)
P = int(str(p) + str(q))
Q = int(str(q) + str(p))
PP = int(str(P) + str(Q))
QQ = int(str(Q) + str(P))
if isPrime(PP) and isPrime(QQ):
break
If we let x, y = len(str(p)), len(str(q)), we will get:
Also we let x', y' = len(str(P)), len(str(Q)), we will get:
After we put $P = 10^{x}p + q,\, Q = 10^{y}q + p$ into the above equation and calculate
\[N=PP \cdot QQ\]we will find $N$ looks like in this form:
\[N = 10^{x+x'+y+y'}pq + \ldots +pq\]Since $x+x’+y+y’$ is big enough, so we know that str(N)[:?] is actually str(pq)[:?] and as the same, str(N)[?:] is actually str(pq)[?:].
After generating my own testcase, I find that str(N)[:18] = str(pq)[:?], str(N)[-18:] = str(pq)[-18:] and actually len(str(p*q)) = 38 so we just need brute force 2 number between the high-part and low-part.
So we can get $pq$ and factor it to get $p$ and $q$. The next is simple decryption.
from Crypto.Util.number import *
from tqdm import tqdm
def decrypt_RSA(c, e, p, q):
phi = (p-1) * (q-1)
d = inverse(e, phi)
m = pow(c, d, p*q)
print(long_to_bytes(m))
n = 98027132963374134222724984677805364225505454302688777506193468362969111927940238887522916586024601699661401871147674624868439577416387122924526713690754043
c = 42066148309824022259115963832631631482979698275547113127526245628391950322648581438233116362337008919903556068981108710136599590349195987128718867420453399
low = str(n)[-18:]
high = str(n)[:18]
pq_prob = []
for i in range(10):
for j in range(10):
pq_prob.append(int(high + str(i) + str(j)+ low))
for x in tqdm(pq_prob):
f = factor(x)
if (len(f) == 2 and f[0][0].nbits() == 64):
p, q = f[0][0], f[1][0]
break
P = int(str(p) + str(q))
Q = int(str(q) + str(p))
PP = int(str(P) + str(Q))
QQ = int(str(Q) + str(P))
N = PP * QQ
print(N == n)
decrypt_RSA(c, 65537, PP, QQ)
Flag
CCTF{wH3Re_0Ur_Br41N_Iz_5uP3R_4CtIVe_bY_RSA!!}