ECDSA Side Channel Attack: Projective Signatures Ledger Donjon CTF Writeup
This challenge involved a special side channel attack on elliptic curve cryptography. It was one of the hardest challenges in the Ledger Donjon CTF. Writeup by esrever and joachim.
Projective Signatures (500pts)
Note: projective coordinate in this writeup refers to Jacobian coordinate.
The challenge
I’m spending a lot of time on this board that computes ECDSA signatures on secp256k1, with an unknown private key.
Using my favorite oscilloscope, I was able to capture what I think is the computation of this signature.
The public key, written in base 10 is (94443785317487831642935972645202783659685599642218408192269455854005741686810,78142542704322095768523419012865788964201745299563420996262654666896320550926).
I was able to get a lot of signatures of the same message, and to record a power trace each time. Using signature verification, I was able to also retrieve the resulting curve point P each time.
My reasonable assumption is that the developers used the usual formulas: point addition and point doubling
After some time analyzing the traces, I have come to the conclusion that the implementation is really well protected, as I couldn’t find any meaningful signal relative to these operations.
However, a small window of several thousands of points seems to be exploitable. This leakage occurs right after the numerous similar patterns of the scalar multiplication, and they should hence correspond to the conversion of the point from a projective coordinates representation to an affine coordinates representation.
Once again, I have a reasonable assumption that the algorithm used to perform the inversion of the Z coordinate is the classic extended binary GCD, that is described for example in Algorithm 1. here.
I don’t have any idea what to do of all this, but I really need this private key!
I extracted from my traces the relevant window. You can download the resulting campaign as an hdf5 file here.
Can you help me retrieve the private key?
The challenge description is quite long, but basically we need to break ECDSA by exploiting extended GCD used for transforming projective coordinates. We also get the following update.
The description of Projective Signatures has been updated to add a precision about the underlying algorithm: The scalar multiplication algorithm is probably performed left to right, bit by bit, as a sequence of double and add operations.
This confuses us for a while: the original description says that the implementation of point addition and point doubling are well protected, but the clarification talks about scalar multiplication. Does that mean they are not really “well protected”? Also, suppose we can get back the projective coordinates by exploiting extended GCD, is there a way to get nonce k by comparing projective coordinates of G and k * G?
It turns out that we are asking the correct questions and we quickly find a paper dealing with almost the same problem: “From A to Z: Projective coordinates leakage in the wild”. The summary of the attack roadmap is:
- Side-channel attack during the computation of $Z^{−1} \mod p$.
- Apply the projective coordinates attack to leak some low bits of nonces.
- Lattice attack for private key recovery.
Side-channel attack for $Z^{-1}$

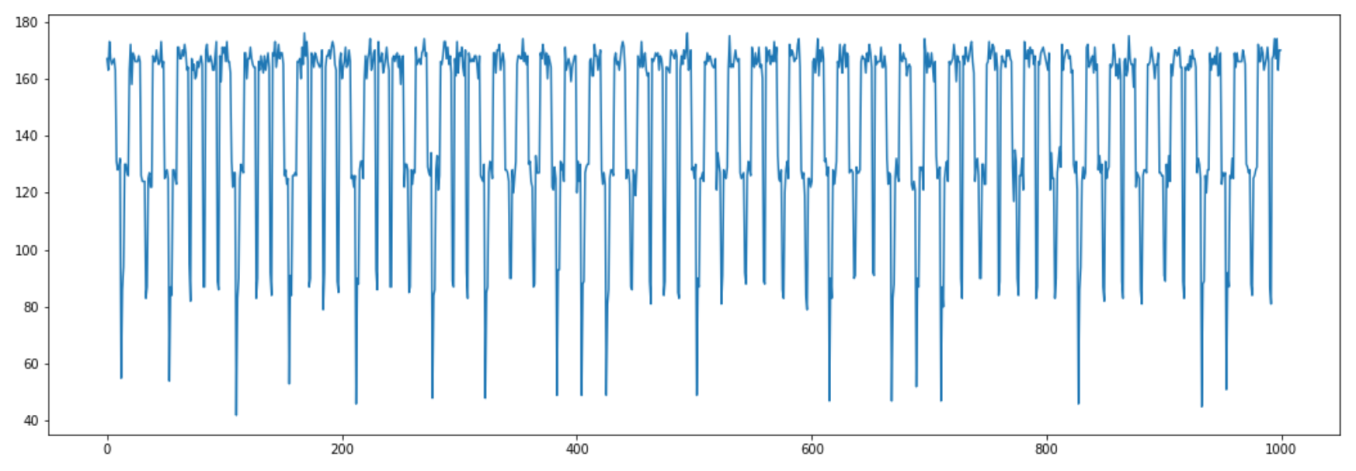
Here is the extended binary GCD mentioned in the description and part of the given traces. It takes us some time to understand the traces and thus to recover the projective coordinates. Here is our thought process along with the observations:
- There are three types of negative spike: long and wide, short and wide, short and narrow.
- The traces seem to start with a long-wide or short-narrow spike.
- There are about 360 spikes for each trace. This is close to 1.5 spike per input bit (the input is 256-bit). We think that the number of iterations is roughly the same as the size of input - which is wrong - and guess that there is one spike for an even
aand two spikes for the odd case. - The traces end with a short-wide spike!
- After some experiments, we find that the number of iterations is actually around 360, so it should probably be one spike per iteration:
- short-narrow => a is even
- short-wide => a is odd and a >= b (no swap)
- long-wide => a is odd and a < b (swap)
With this, we are able to consistently recover the input of the extended binary GCD. However, it seems that the inverse is taken against the elliptic group size rather than the field characteristic. Luckily, the problem setter confirm that it is a mistake on their side and release a new set of traces.
Here is the script to recover the projective coordinates. It does not work for some traces because of premature thresholds, but it finds enough coordinates for the attack.
import h5py
def find_large_gaps(trace, value_threshold=70, gap_size_threshold=40):
gaps = []
last_change = 0
for i in range(1, len(trace)):
is_changed = (trace[i - 1] < value_threshold <= trace[i]) or \
(trace[i] < value_threshold <= trace[i - 1])
if is_changed:
if trace[i] >= value_threshold and i - last_change > gap_size_threshold:
gaps.append((last_change, i))
last_change = i
return gaps
def find_range(trace):
gaps = find_large_gaps(trace)
assert len(gaps) == 2, (gaps, trace)
return gaps[0][1], gaps[1][0]
def get_spikes(trace):
start, end = find_range(trace)
core_trace = trace[start: end]
gaps = find_large_gaps(core_trace, value_threshold=145, gap_size_threshold=1)
spikes = []
for le, ri in gaps:
is_wide = ri - le > 5
is_long = min(core_trace[le: ri]) < 70
if is_long:
spikes.append('l')
elif is_wide:
spikes.append('s')
else:
spikes.append('.')
return ''.join(spikes)
def construct_from_spikes(spikes):
a, b = 0, 1
for spike in spikes[::-1]:
if spike == '.':
a <<= 1
elif spike == 's':
a = a * 2 + b
assert a & 1, (a, b, spike, spikes)
else:
a = a * 2 + b
a, b = b, a
assert a & 1, (a, b, spike, spikes)
assert b & 1, (a, b, spikes)
return a, b
def get_z_coordinate(trace):
z, p = construct_from_spikes(get_spikes(trace))
assert p == 115792089237316195423570985008687907852837564279074904382605163141518161494337, (z, p)
return z
data = h5py.File('all_signatures.h5', 'r')
with open('zs.txt', 'w') as f:
for i in range(0, 100000):
z = get_z_coordinate(data['leakages'][i])
f.write(str(z) + '\n')
Projective coordinates attack
Trying to leak information of nonce with elliptic point itself is probably as hard as solving the discrete logarithm problem, but knowing the projective representation of scalar multiplication allows us to easily obtain some information. This is the main idea of projective coordinate attack.
In a classic double-and-add algorithm, different operations are performed for zero and one bits, leading to different algebraic properties in the projective representation.
Given a projective representation of a point $P = (X_0, Y_0, Z_0)$, we want to know if it comes from $double(X_1, Y_1, Z_1)$ or $add_G(X_1, Y_1, Z_1)$. We write $(x_1, y_1) = (X_1 / Z_1^3, Y_1 / Z_1^2)$ for the affine representation of the input point. Once we fix the operation to be $double$ or $add_G$, we can reverse it and compute $(x_1, y_1)$ (but $Z_1$ remains undetermined).
Suppose $P$ is from $double$, we have the relation
\[Z_1 = \sqrt[4]{\frac{Z_0}{2y_1}}.\]On the other hand, if it is from $add_G$, we have
\[Z_1 = Z_G^{-1} \cdot \sqrt[3]{\frac{Z_0}{2(x_G - x_1)}},\]where $(x_G, y_G)$ and $(X_G, Y_G, Z_G)$ are the affine and projective representation of the generator $G$. We assume $Z_G = 1$.
By checking the existence of 4th root and cube root, we can rule out the possibility of one of the operations. We do it recursively and leak the bit(s) until the check doesn’t tell us anything.
Following is the population of nonce bits leaked. The distribution is similar to that in the paper, except for 6 leaked bits. We confirm with the problem setter that there is an intentional bias in the generated nonces, causing the anomalous figure.
| # leaked bits | Population |
|---|---|
| 0 | 32960 |
| 1 | 52423 |
| 2 | 9041 |
| 3 | 3011 |
| 4 | 1051 |
| 5 | 353 |
| 6 | 1107 |
| 7 | 37 |
| 8 | 10 |
| 9 | 3 |
| 10 | 2 |
| 11 | 2 |
Here is our Sage script for the projective coordinates attack.
p = SECP256k1.curve.p()
a = SECP256k1.curve.a()
b = SECP256k1.curve.b()
F = GF(p)
E = EllipticCurve(F, [a, b])
Gx = SECP256k1.generator.x()
Gy = SECP256k1.generator.y()
G = E(Gx, Gy)
def leak_k(points, k=[]):
if len(k) == 6:
return k
flag = 0
next_points = []
for x0, y0, Z in points:
if flag == 3:
return k
X0, Y0, Z0 = F(x0 * Z**2), F(y0 * Z**3), F(Z)
# k0 == 0
r0 = E(x0, y0)
r1 = r0.division_points(2)
assert len(r1) == 1
x1, y1 = r1[0].xy()
Z1s = (Z0 / F(2 * y1)).nth_root(4, all=True)
if Z1s:
flag |= 1
for Z1 in Z1s:
next_points.append((x1, y1, Z1))
# k0 == 1
xt, yt = (r0 - G).xy()
Zts = (Z0 / 2 / (F(Gx) - xt)).nth_root(3, all=True)
r1 = (r0 - G).division_points(2)
assert len(r1) == 1
x1, y1 = r1[0].xy()
if not Zts:
continue
for Zt in Zts:
Z1s = (Zt / F(2 * y1)).nth_root(4, all=True)
if Z1s:
flag |= 2
for Z1 in Z1s:
next_points.append((x1, y1, Z1))
if flag == 0:
return k
elif flag == 1:
return leak_k(next_points, k + [0])
elif flag == 2:
return leak_k(next_points, k + [1])
else:
return k
for i in range(100000):
Z, order = get_z_coordinate(data['leakages'][i])
if order != SECP256k1.order:
continue
digest, sig_r, sig_s, kGx, kGy = parse_signature(data["values"][i])
k = leak_k([(kGx, kGy, F(Z))])
print(k)
Recover private key
After we retrieved the nonce bits, the final step is to perform a lattice attack to recover the private key. As mentioned in section 6.3 of the paper, this recovery problem can be formulated as the Hidden Number Problem. When implementing the attack as described, there is still one catch: in lbgcrypt a nonce is padded as follows: $k = \hat{k} + \rho n$, with $\rho = 1$ for secp256r1.
Although we could have brute-forced the $\rho$ value if necessary, we decided to check with the challenge author. In this case, $\rho = 0$, so the lattice implementation is slightly different. The rest of the attack is straightforward to implement using Python and Sage.
from sage.all import EllipticCurve
from sage.all import GF
from sage.all import Matrix
from sage.all import QQ
from sage.all import inverse_mod
import h5py
import random
# secp256r1 curve specification.
E = EllipticCurve(GF(0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F), [0, 7])
G = E(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8)
n = int(G.order())
# Rho value is 0 in this case.
rho = 0
public_key = E(94443785317487831642935972645202783659685599642218408192269455854005741686810, 78142542704322095768523419012865788964201745299563420996262654666896320550926)
# Implementation of the lattice attack
def lattice_attack(signatures, n):
# signatures[i][0] = h (digest)
# signatures[i][1] = r (r value of signature)
# signatures[i][2] = s (s value of signature)
# signatures[i][3] = c (known bits)
# signatures[i][4] = l (known bitsize)
m = len(signatures)
# Filling in the diagonal of the lattice.
B = Matrix(QQ, m + 2)
for i in range(m):
l = signatures[i][4]
B[i, i] = 2 ** (l + 1) * n
# Filling in the second to last row of the lattice.
for i in range(m):
r = signatures[i][1]
s = signatures[i][2]
l = signatures[i][4]
t = int(r * inverse_mod(2 ** l * s, n)) % n
B[m, i] = 2 ** (l + 1) * t
B[m, m] = 1
# Filling in the last row of the lattice.
for i in range(m):
h = signatures[i][0]
s = signatures[i][2]
c = signatures[i][3]
l = signatures[i][4]
a = (c - rho * n) % (2 ** l)
u = int((a - h * inverse_mod(s, n)) * inverse_mod(2 ** l, n)) % n + QQ(n / (2 ** (l + 1)))
B[m + 1, i] = 2 ** (l + 1) * u
B[m + 1, m] = 0
B[m + 1, m + 1] = n
print("Executing LLL")
B = B.LLL()
for row in B.rows():
private_key = int(row[m]) % n
if private_key * G == public_key:
return private_key
# Reading the nonce bits recovered in step 2.
with open("nonce_bits", "r") as f:
nonce_bits = list(map(eval, f.readlines()))
# Reading the provided signature data.
data = h5py.File("all_signatures.h5", "r")
values = data["values"]
signatures = []
for i, bits in enumerate(nonce_bits):
# We're only interested in the cases where we know at least 6 nonce bits.
# This reduces the time necessary for the lattice attack.
if len(bits) >= 6:
h = int.from_bytes(bytes(values[i][0]), "big")
r = int.from_bytes(bytes(values[i][1]), "big")
s = int.from_bytes(bytes(values[i][2]), "big")
c = 0
l = len(bits)
signatures.append((h, r, s, c, l))
print(f"Found {len(signatures)} signatures")
# 200 random signatures should be enough for the lattice attack.
# We could play it safe, and use all 1000+ signatures, but this would take more time.
random.shuffle(signatures)
private_key = lattice_attack(signatures[:200], n)
print(f"Private key: {private_key}")
Finally, with the private key 15847465188978300083942528449491794939171261456473785532093406410497100707097 we can executed the provided decrypt_flag.py script.
This gives us the flag: CTF{0n(3464!n1|=a|_|_1nToMy|*|?0j3ct1v3w4y5....} (“Once again I fall into my projective ways….”).